Вычислите. Алгебра 9 класс.
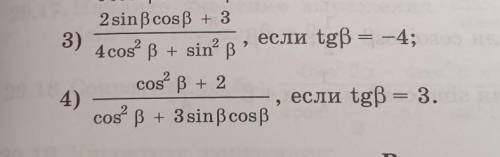
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти производную функцию y=x/(a*√(a^2+x^2))...
3 - Найти производную функцию y=(x^2+1)/(x^2-4)...
2 - Найти производную функцию y=2x^3-3x^2+15...
1 - Определить молярность 49% фосфорной кислоты (плотность 1,33 г/мл)....
1 - Скільки грамів молочної кислоти утвориться при бродінні 50 г глюкози?...
1 - C+ co - бывает такое? если да, то что?...
2 - Найти значение выражения : 1 - 2 sin 150 °...
1 - Найти площадь фигуры, ограниченной линиями: y=x+1, y=5 + 3x-2x2...
3 - Найти площадь фигуры, ограниченной линиями: y=x+1, y=5 + 3x-2x2...
1 - 1. у человека ген карих глаз доминирует над геном голубых глаз. голубоглазый...
2
Объяснение:
3) а)
б) Подставим (-4 cos b) вместо sin b
4)
Подставим (3 cos b) вместо sin b