Вычислите:
1)log₂14 - log₂7=
2)log₃36-log₃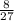 $\frac{8}{27}$ +log₃18=

Решите уравнения:
1)log₂( х−3) = log₂10;
2)log₃(1−6 х) = log₃(17-х²)=

Решите неравенство:
log₃(3 х−1)>log₃(2 х+3).

Ответы

roman81rudi 01.01.2021 21:34

$1)log_{2}14-log_{2}7=log_{2} \frac{14}{7} =log_{2}2=\boxed1\\\\2)log_{3}36-log_{3}\frac{8}{27} +log_{3} 18=log_{3} (36:\frac{8}{27}*18)=log_{3}(36*\frac{27}{8}*18)=\\\\=log_{3}2187= log_{3}3^{7}=7log_{3}3=\boxed7$

1)ОДЗ : x - 3 > 0 ⇒ x > 3

$log_{2}(x-3)=log_{2}10\\\\x-3=10\\\\\boxed{x=13}$

$2)log_{3}(1-6x)=log_{3}(17-x^{2})\\\\1-6x=17-x^{2}\\\\x^{2}-6x-16=0\\\\x_{1} =-2\\\\x_{2} =8\\\\Proverka:\\\\1)1-6*(-2)=1+12=130\\17-(-2)^{2}=17-4=130\\\\2)1-6*8=1-48=-47$

$ODZ:\\\left \{ {{3x-10} \atop {2x+30}} \right.\\\\\left \{ {{3x1 } \atop {2x-3}} \right.\\\\\left \{ {{x\frac{1}{3} } \atop {x-1,5}} \right.\Rightarrow x\frac{1}{3} \\\\log_{3}(3x-1)log_{3}(2x+3)\\\\3x-12x+3\\\\3x-2x3+1\\x4\\\\Otvet:\boxed{x\in(4;+\infty)}$

Вычислите: 1)log₂14 - log₂7= 2)log₃36-log₃+log₃18= Решите уравнения: 1)log₂( х−3) = log₂10; 2)log₃(1

ПОКАЗАТЬ ОТВЕТЫ

sernikovs 01.01.2021 21:34

Данный ответ представлен фотографией.

ПОКАЗАТЬ ОТВЕТЫ

gfsggstgf 18.01.2024 19:12

Добрый день! Давайте рассмотрим каждую задачу по порядку.

Выражение 1) log₂14 - log₂7 можно упростить с помощью свойств логарифмов. Одно из свойств логарифмов гласит, что вычитание логарифмов с одинаковым основанием эквивалентно взятию логарифма от частного. То есть, log₂14 - log₂7 = log₂(14/7) = log₂2 = 1.

Выражение 2) log₃36 - log₃ $\frac{8}{27}$ + log₃18 можно также упростить с помощью свойств логарифмов. Здесь мы воспользуемся свойством, которое гласит, что разность логарифмов с одинаковым основанием эквивалентна взятию логарифма от частного. То есть, log₃36 - log₃ $\frac{8}{27}$ + log₃18 = log₃(36/( $\frac{8}{27}$ *18)).

Для упрощения дроби 36/( $\frac{8}{27}$ *18), мы можем сократить числитель и знаменатель на их общий делитель. Общий делитель в данном случае это 18, поэтому дробь станет равна 2/8 = 1/4.

Итак, log₃(36/( $\frac{8}{27}$ *18)) = log₃(1/4). Логарифм от 1/4 по основанию 3 можно записать как -log₃4. Таким образом, выражение становится равным log₃4.

Теперь перейдем к решению уравнений.

Уравнение 1) log₂(х−3) = log₂10 может быть решено с помощью свойства, которое гласит, что равенство двух логарифмов с одинаковым основанием эквивалентно равенству аргументов. То есть, х−3 = 10. Решив это уравнение, мы получим х = 13.

Уравнение 2) log₃(1−6х) = log₃(17-х²) может также быть решено с помощью свойства равенства логарифмов. По свойству аргументов логарифма, мы можем записать уравнение в следующем виде: 1−6х = 17-х². Перенеся все члены в правую сторону, мы получим квадратное уравнение -х²+6х+16 = 0. Решая это уравнение, мы получим два решения: х = 2 и х = 8.

Для решения неравенства log₃(3х−1) > log₃(2х+3) мы можем использовать свойство монотонности логарифма, которое гласит, что если основание логарифма больше 1, то логарифм монотонно возрастает. В данном случае основание равно 3 и больше 1, поэтому мы можем убрать логарифмы и записать неравенство в следующем виде: 3х-1 > 2х+3. Перенеся все члены в одну сторону, мы получим х > 4.

Итак, решение неравенства log₃(3х−1) > log₃(2х+3) это х > 4.

Надеюсь, это объяснение помогло вам понять решение данных задач. Если у вас возникли ещё вопросы, не стесняйтесь задавать их!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра