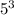вычислить значение выражения
Другие вопросы по теме Алгебра
Популярные вопросы
- сумму 168030 записать в виде разрядных чисел...
2 - Вычисли массу углерода, содержащегося в карбоновой кислоте C17H33COOH...
1 - подставить Past tenses вместо инфинитивов: 1. Yes, Hattie? What...
2 - Найдите общее решение дифференциального уравнения:...
1 - 10 во и ответов про рептилий и амфибий...
3 - К раствору сахара массой 200г с массовой долей сахара 20% добавили...
1 - Согласованные / несогласованные приложения. Как правильно? Сюжет...
2 - Назвіть ознаки казки у творі Маленький принц напишіть це контрольна...
3 - Металічні властивості графіту....
1 - На 12.8г міді подіяли надлишком концентрованої сульфатної кислоти....
1
125
Объяснение:
Для начала поднесём скобки к степеню:
Теперь сократим делённое:
Теперь произведём деление:
Деление на дробь это умножение на перевёрнутый дробь
Сокращаем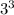 и
и 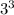
Розписываем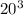 как
как 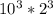
Сокращаем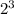 и
и 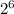
Розписываем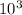 как
как 
Сокращаем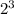 и
и 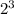
В результате получаем