Вычислить Sin (α+ β), Cos (α – β), Cos 2β, Sin 2α, tg2α, если...
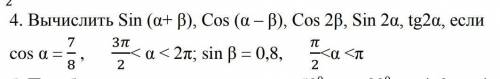
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему 3 закон ньютона не выполняется для магнитной силы?...
2 - Ауіпсіздік сенімхатты мұғалімдер бақытгүл создерге фонологиялық...
2 - Какое число нужно написать вместо x, чтобы равенства были верными...
3 - 8кг 9. ? кг 17 кг б) составь и реши обратные , используя таблицу....
1 - Шесть рабочих за 5 дней могут изготовить 120 деталей. сколько...
1 - Используя график зависимости пути от времени, расчищайте с какой...
3 - Условие одно, но мой вариант с лева. ...
1 - Кошка китти весит на 3 килограмма больше кошки машки, а кошка...
1 - Составить диалог используя слова sorry,and you,excuse me,really?...
2 - Найдите полную поверхность шара, если r=3, 4см...
3
угол а принадлежит 4 четверти => sina отрицательный
угол в принадлежит 2 четверти => cosв отрицательный.
Нашли необходимое, перейдём к вопросам задания.