Вычислить производные функции
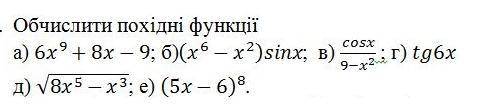
Другие вопросы по теме Алгебра
Популярные вопросы
- спробуйте використовуючи дієслова створити свій вірш-жарт про зустріч ваших...
1 - Чем отличается маркетолог от таргетолога...
2 - Насыпали 9 мешков пшеницы по 80 кг каждый и 7 мешков ржи по 60 кг на сколько...
2 - Казахстан очень красивый город. В нём много наций.Здесь много достопримечательностей.И...
1 - Складіть рівняння реакцій галогенів: а) з барiєм; б) цинком; в) алюмініем; г)...
2 - Кто были родители Февронии?...
1 - Один один из смежных углов больше другого на 30 градусов Найдите смежные углы...
2 - Разбейте по метрам, сантиметрам,и дециметрам: « 3654см »...
1 - Сравните числа: √ 23 + √ 14 и √ 37 Решите уравнение a) |2x-3|=7 б) |x^2 -8|=2x...
2 - и нарисуйте график только так чтобы точки на графике были видны что соединять...
3
Объяснение:
а) f'(x)= 54x⁸+8
б) f'(x)= (x⁶-x²)'sin(x)+(x⁶-x²)*(sin(x))'= sin(x)*(6x⁵-2x)+cos(x)(x⁶-x²)= sin(x)*2x(3x⁴-1)+cos(x)*x²(x⁴-1)
в) f'(x)= (cos(x)'(9-x²)-cos(x)*(9-x²)')/(9-x²)²= (-sin(x)(9-x²)+cos(x)*2x)/(9-x²)²
г) f'(x)= 6/cos²(6x)
д) f'(x)= 1/2√8x⁵-x³ * (40x⁴-3x²)= (40x⁴-3x²)/2√8x⁵-x³
е) f'(x)= 8(5x-6)⁷*5= 40(5x-6)⁷