Вычислить площадь фигуры, ограниченной линиями y= 4х-х² , y =5, x=3, х =0.
Другие вопросы по теме Алгебра
Популярные вопросы
- ответить на вопрос по рассказу лескова человек на часах : как...
1 - Критиковать почему после р и, а не е...
2 - Кто написал скаку про огурчика и помидорка...
1 - За подробное (верное! ) решение 50 ! 1. 2....
3 - Биссектрисы углов в и с треугольника авс продолжили до пересечения...
1 - Предложения в переносном смысле из сказок (нужно 3)...
1 - Сбиографией прокофьева. 1)назовите важнейшие жизни прокофьева?...
1 - Сочинение на тему как я путешествовал этим летом большое примерно...
1 - Укажите фразеологизм, который возник из пьесы шекспира гамлет...
3 - Определите количество вещества,содержащегося в 26,88л (н.у.)...
2
Вычислим определённый интеграл. Это и будет ответом.
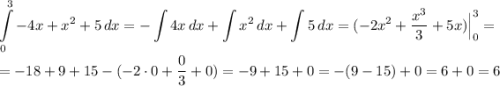
ответ: