Вычислить площадь фигуры, ограниченной линиями y=-2x-x²,y=0
Ответы
Найдем точки пересечения графиков:
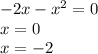


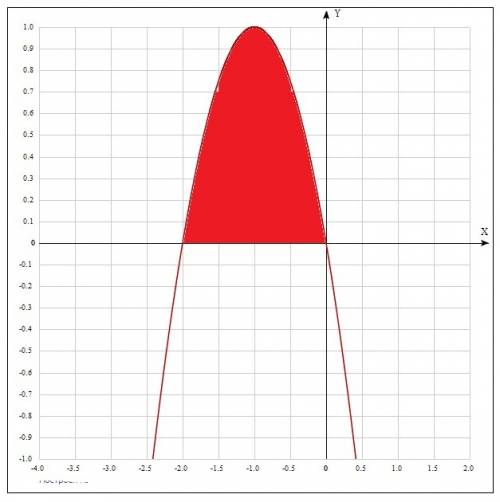
ПОКАЗАТЬ ОТВЕТЫ
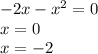



Другие вопросы по теме Алгебра
Популярные вопросы
- Докажите тождество 2^2+6^2++(4n-2)^2=4n(2n-1)(2n+1) разделить на 3....
3 - Найти среднию скорость за первые 6 сек...
1 - Вдвух одинаковых купейных вагонах поезда 72 места.сколько мест в 5 таких купейных...
1 - Метрология. напишите неравенство для размера длины (l) при заданной точности измерения...
3 - Никрасов как писатель относится к детям запиши опять я в деревне. хожу на охоту,...
3 - Изобразите на координатной плоскости множество точек,координаты которых (x; y)...
3 - Метрология. правила выбора стандартов...
3 - Центральная нервная система состоит из...
3 - X-2| x 3=x+8 |-это модуль если что x3-это умножить на три...
1 - Достон ли принц генрих прозвища почётного мореплавателя?...
2