Вычислить площадь фигуры, ограниченной линиями
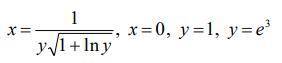
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) Назовите наиболее крупные формы рельефа Северной Америки. Каково их...
2 - Геометрия ответить на во если можно , подробно ) ,...
2 - По схеме, изображённой на рисунке 2, определите сопротивления R2...
3 - P=50кПа F=5Н S=? решение задачи...
1 - Щербакова уходит в отпуск по беременности и родам в марте 2018.Продолжительность...
3 - Как получают Проволоку толщиной до 5 мм...
2 - Які стихійні явища характерні для степової зони Пн. Америки. Обгрунтуйте...
3 - Библиотекарь получила школьные учебники и решила разместить их по стеллажам....
1 - Какие виды термометров ты знаешь? Каким термометром можно измерить температуру...
2 - Зачеркни лишнее словосочетание письменно объяснив свой выбор Золотые украшения...
2
2
Объяснение:
Учитывая, что функция содержит логарифм, то y>0, а значит и x>0.
То есть х изменяется как
Также по условию, 1≤y≤e³
Тогда искомая площадь найдется как