Вычислить ординату точки графика функции y=2x2−3x+1, в которой касательная к этому графику параллельна прямой y=3x+7.
Zoya20060609
2
03.10.2019 12:26
1
Другие вопросы по теме Алгебра
Мама1мама2
11.05.2021 23:30
Alinkass93
11.05.2021 23:29
vladsunygin
11.05.2021 23:29
annafilimonova1
11.05.2021 23:26
leontievasv
11.05.2021 23:25
nakiba321
11.05.2021 23:25
katyat1510
11.05.2021 23:23
вика3877
11.05.2021 23:21
DanilZ2
21.03.2020 22:49
Популярные вопросы
- На сковорiдку вмiщаються 2 шматки хлiба. щоб пiдсмажити шматок хлiба з одного боку...
3 - 1)в перевозимом грузе 240 кг яблок и 120 кг груш.постройте круговую диаграмму распределения...
3 - Найди значения выражений 38+62 100-100 17+64 93-0 5*10 0: 4 8*9 64: 8 12+0 100:...
2 - Япострою изо льда крепости и в слове 6 букв что за слова пропущено....
1 - Ккакой горной системе, хребту или нагорью относится килиманджаро?...
3 - Для детского сада купили по одинаковой цене 46 метров жёлтого шёлка и 32 метра...
1 - Решить уравнение методом введения новой переменной: х6-63х3-64=0...
2 - 2по сімейному праву и 2 по житловому праву, з відповідями...
1 - Прочитайте.вспомните,из какой сказки пушкина эти строки. ветер,ветер! ты могуч,...
2 - Расставьте знаки препинания учитель евгений николаевич спокойный заботливый и трудолюбивый...
3
Пусть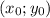
- координаты точки касания касательной.
Производная данной функции: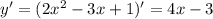
Поскольку касательная параллельна прямой y = 3x + 7, то у них угловые коэффициенты равны, а тогда по геометрическому смыслу производной, мы получим
Тогда ордината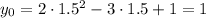
ответ: 1.