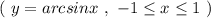Вычислить определенные интегралы. а)Используя основные свойства и формулы
б )методом подстановки
с)методом интегрированием по частям
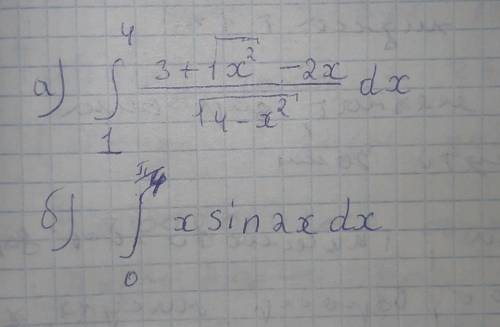
Другие вопросы по теме Алгебра
Популярные вопросы
- Перестройте предложения, раскрыв скобки. приобрели 22 (пассатижи), 23 (ножницы),...
1 - Can you complete each space with one word....
2 - Нужна ваша мне надо составить сочинение на тему описание внешности моей подруги...
3 - Все решить я уже два часа сижу над и это последние...
2 - катети прямокутного трикутника відносяться, як 5: 12. обчислитипериметр трикутника,...
1 - Уэллс.г. человек невидимка отзыв...
3 - Начерти отрезок, который на 2 см короче данного отрезка...
3 - 11 пар(-ы) туфель стоят в магазине 8701 рублей. сколько нужно заплатить за...
3 - Точка висоти, опущеної на основу рівнобедреного трикутника,рівновіддалена від...
3 - Нужна ! зробіть повний фонетичний аналіз слова: взаємозв’язок....
3
Вычислить определённый интеграл невозможно, так как не существует arcsin2