Вычислить криволинейный интеграл по координатам
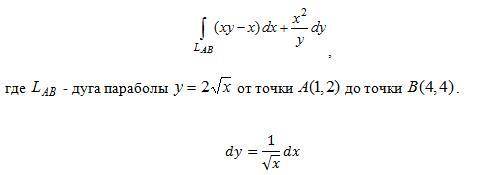
Другие вопросы по теме Алгебра
Популярные вопросы
- Может ли высказывание быть сформулировано в вопросительном или...
2 - Запишите числа предшествующие числам 90 80 70 60 50 40 40 30 20...
2 - Расскажите о значении художественной культуры античности. примеры...
2 - Нужно составить по одному предложению с каждым союзом..союзы-wer,als,nach,den...
3 - Напиши три числа так чтобы сумма любых двух соседних чисел была...
2 - 10 правил о моей семье! ! заранее...
3 - Найдите количество чисел ,взаимно простых с числом 21 и удовлетворяещему...
1 - Какая идея сближала славянофилов и революционеров-демакратов...
3 - Нужно составить по 3 причастие+существ. местоимение+существ. глагол+существ....
2 - Замени повторяющиеся слова синонимами. костя вышел из дома рано...
2
421/20
Объяснение:
Имеем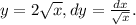 Подставим данные выражения в подынтегральное и будем интегрировать по направлению x от 1 до 4:
Подставим данные выражения в подынтегральное и будем интегрировать по направлению x от 1 до 4: