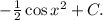Вычислить интеграл ∫xsinx²dx так, чтобы было понятно, что откуда взялось
Другие вопросы по теме Алгебра
Популярные вопросы
- частота колебаний крыльев шмеля 200 гц.сколько взмахов крыльями...
3 - 1. Написать определения следующим словам: Person- policeman,...
1 - Математика номер 9 , 89бет...
3 - за подробное решение В треугольнике ΔPRT на стороне PR взяли...
2 - Ознакомьтесь с текстом Статьи 5 (Соблюдение и уважение прав...
2 - a) Длину стороны AB; б) уравнение стороны AB; в) уравнение медианы...
1 - Выручитеоси симметриицентр симметриии оси, и центр симметрии...
3 - А. П. Чехов рассказ Мальчики 1вопрос.опишите внешность Володи...
2 - А)какую часть составляют 3 см в квадрате от квадратного метра?...
2 - Биология 8 класс. Пасечник, Каменский, Швецов. Параграф 26 (конспект...
3
Обозначим данный интеграл буквой I.
Обратим внимание на конструкцию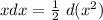
Тогда интеграл примет вид:
Теперь для удобства заменим x² = t:
Вернемся к переменной х:
ответ: