Вычислить интеграл,
∫ √(x³-7)*3x² dx.
сложная тема
Другие вопросы по теме Алгебра
Популярные вопросы
- Эссе 40 сөз қазіргі заман эссе написать...
1 - Найдите значение выражения (3+ корень квадратный из семи) в квадрате...
1 - Луч sc является биссектрисой угла s а отрезок sa и sb равны.докажите...
1 - Запишите предложения, включив в них вводные слова со значением...
3 - Автомабиль за 3 ч проехал 240км.на сколько нужно уменьшить скорость...
1 - Чем покрытосеменные растения отличаются от голосеменных...
1 - Составить 3 словосочетания с предлогами , согласно, вопреки (они...
2 - Ознакомьтесь с предложенной ситуацией: - 6-й класс языковой гимназии....
3 - Сдокладом по . война 17-18 вв. в европе. : соберите информацию...
2 - 3.какое государство вступило в войну в мае 1877 г.на стороне россии?...
2
∫ √(x³-7)*3x² dx =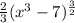 + С, С - константа
+ С, С - константа
Объяснение:
По правилам расчета производных, производная от
т.е.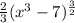 +С является первообразной для √(x³-7)*3x²
+С является первообразной для √(x³-7)*3x²