Вычислить: (и если можно распишите как это решается) а) log₃2+log₃4.5=; б) (lg27-lg3)/(lg15-lg5)=; в) (ln18+ln8)/2ln₂+ln3)=
Другие вопросы по теме Алгебра
Популярные вопросы
- 30 тело брошено вертикально вверх по закону h= v0t-gt^2/2. найдите через...
2 - Обговоріть ситуації та, використовуючи норми законодавства, прийміть рішення...
3 - Вставьте тект прилагательные lastig, originell, auslandisch, reichhaltig,...
3 - 20 .га тело в противоположных направлениях действует две силы f1=2h и f2=4h.вычислете...
2 - Запишите название любого объекта (города, населённого пункта, реки или который...
3 - Встихотворении п.васильева иртыш„ рассказывается о.. основную мысль стихотворения...
1 - Use the endings below to make adjectives from the group of words (a-k)....
3 - Последовательность задана формулой yn = n/n+1 вычислите десять первых членов...
2 - Постройте домик в pascal.net напишите кординаты ()...
1 - Уподножья горы барометр показывает 642 па,а на вершине горы 90 317па определите...
2
б)(lg27-lg3)/(lg15-lg5)=(lg(27:3))/(lg(15:5))=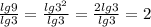
в)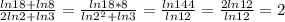
a) log₂2+log₂4,5=log₂2*4,5=log₂9