1. Алгебра
  2. Вычислить cos3α/cosα, если

Вычислить cos3α/cosα, если известно, что 2sin3α=sinα

olga170103 olga170103    2   30.01.2022 17:56    1

Ответы
TimaWarface TimaWarface  30.01.2022 18:00

Формулы синуса и косинуса тройного угла:

\sin3x=3\sin x-4\sin^3x

\cos3x=4\cos^3x-3\cos x

Рассмотрим известное равенство:

2\sin3\alpha =\sin\alpha

2(3\sin\alpha-4\sin^3\alpha ) =\sin\alpha

6\sin\alpha-8\sin^3\alpha =\sin\alpha

5\sin\alpha-8\sin^3\alpha =0

\sin\alpha(5-8\sin^2\alpha) =0

Возможны две ситуации:

\sin\alpha=0\Rightarrow \sin^2\alpha=0\Rightarrow \cos^2\alpha =1-\sin^2\alpha=1-0=1

5-8\sin^2\alpha =0\Rightarrow \sin^2\alpha =\dfrac{5}{8} \Rightarrow \cos^2\alpha =1-\sin^2\alpha =1-\dfrac{5}{8}=\dfrac{3}{8}

Рассмотрим искомое выражение:

\dfrac{\cos3\alpha }{\cos\alpha } =\dfrac{4\cos^3\alpha -3\cos\alpha }{\cos\alpha } =\dfrac{\cos\alpha(4\cos^2\alpha -3) }{\cos\alpha } =4\cos^2\alpha -3

Зная два возможных значения квадрата косинуса, найдем возможные значения выражения.

При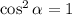 \cos^2\alpha =1:

\dfrac{\cos3\alpha }{\cos\alpha } =4\cdot1 -3=1

При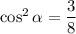 \cos^2\alpha =\dfrac{3}{8}:

\dfrac{\cos3\alpha }{\cos\alpha } =4\cdot\dfrac{3}{8} -3=\dfrac{3}{2} -3=-\dfrac{3}{2}=-1.5

ответ: 1 или -1.5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
2001maks44 2001maks44  11.12.2020 17:59
Представьте в виде произведения выражение 49a²-⅙b⁴(если что ⅙ это дробь)​​...
Pacan4ikForever Pacan4ikForever  11.12.2020 18:00
РЕБЯТ РЕШИТЕ ЗАДАНИЕ В ФОТО!...
bearn2p0dqt1 bearn2p0dqt1  11.12.2020 18:00
Упростите выражение 14x^5 + 23n^6 * (5bc^2 + 6x^3)...
Avmb Avmb  11.12.2020 18:00
Розв яжіть рівняння: (х-2)(х+2)=х²+8х...
ТуристАртемий ТуристАртемий  11.12.2020 18:00
Упрости выражение и найди его значение (x^2-x) - (3x+x^2) при x = 1,2...
nikita1424 nikita1424  11.12.2020 18:00
471.какой угол образуют костельные графика функции в точки с абсциссой. b)...
AnyaFilenkova AnyaFilenkova  28.07.2019 00:50
Хв квадрате - 100 = 0 решите уравнение...
AltoДима AltoДима  28.07.2019 01:00
C^2-a^2+2ab-b^2 разложить на множители...
svetaH666 svetaH666  28.07.2019 01:00
Найдите наименьшее значение выражения (x-7)^2+2...
Bog5635545 Bog5635545  28.07.2019 01:00
6х в квадрате + х - 5 = 0 решите уравнение...

Популярные вопросы