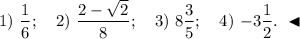Вычислиие интеграл, преобразуя подынтегральные функции
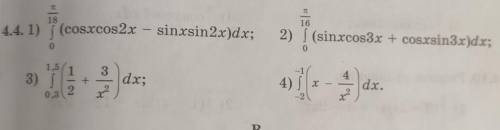
Другие вопросы по теме Алгебра
Популярные вопросы
- Один станок автомат изготавливается один день 200 деталей сколько деталей изготовил...
3 - Выявить художественные средства ( тропы, синтаксические средства) 1. как побил...
3 - Выразите в см 12 м 34 см 6 см 35 дм в мм 8 м 54 см в дм 37000 мм в м 73 мм 5...
3 - Подобрать аргументы к утверждению с. лагерлеф.при бегстве всегда гибнет больше...
1 - Подставь нужное число, что бы пример был правильным -7-( )=-2...
1 - Составьте предложения со словами равнение и сравнять. заранее ....
3 - Масса человека в неподвижном лифте равна 600 н, а в подвижном 540 н. узнать модуль...
3 - Разобрать предложение под ц 4 ты помни об этом, береги книги!...
1 - 4класс вычисли 4 ч 5 минут *2+6ч 15 мин *2 2 км 308 м *2 -6км 90 м : 3 (6ц 5...
2 - Цыфра 2 это по составу разобрать? слово в туманном!...
3
Воспользуемся формулой косинуса суммы: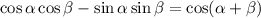
Тогда имеем:
Пусть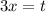 . Тогда
. Тогда 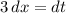
Пределы интегрирования:
еслиПереходим к новому определенному интегралу с новой переменной и пределами интегрирования:
Воспользуемся формулой синуса суммы: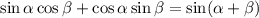
Тогда имеем:
Пусть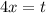 . Тогда
. Тогда 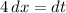
Пределы интегрирования:
еслиПереходим к новому определенному интегралу с новой переменной и пределами интегрирования:
ответ: