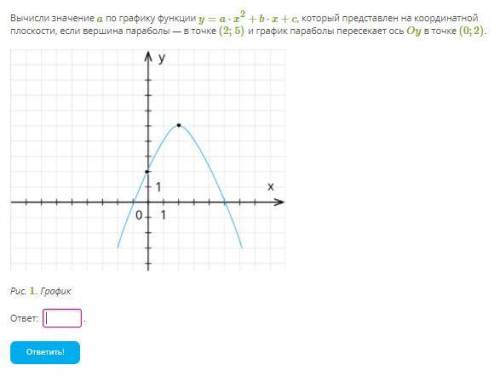
Вычисли значение a по графику функции y=a⋅x2+b⋅x+c, который представлен на координатной плоскости, если вершина параболы — в точке (2; 5) и график параболы пересекает ось Oy в точке (0;2). График 1.png

Рис. 1. График

ответ:

Для вычисления значения переменной a в уравнении y=a⋅x^2+b⋅x+c, нам необходимо использовать известные точки на графике.

Из графика мы видим, что вершина параболы находится в точке (2; 5). Значит, когда x=2, y=5. Подставим эти значения в уравнение параболы:
5=a⋅2^2+b⋅2+c

Также из графика мы видим, что парабола пересекает ось Oy в точке (0; 2). Значит, когда x=0, y=2. Подставим эти значения также в уравнение параболы:
2=a⋅0^2+b⋅0+c

Выполним вычисления:

Уравнение для вершины параболы:
5=a⋅4+b⋅2+c (1)

Уравнение для точки пересечения параболы с осью Oy:
2=c (2)

Из уравнения (2) получаем значение c=2.

Подставим значение c=2 в уравнение (1):
5=a⋅4+b⋅2+2

Раскроем скобки и упростим уравнение:
5=4a+2b+2

Перенесем неконстантные члены в левую часть уравнения:
4a+2b=3

Теперь мы получили систему уравнений:
4a+2b=3 (3)
c=2 (4)

Для решения системы уравнений (3) и (4) нам необходимо использовать два уравнения с двумя неизвестными a и b.

Умножим уравнение (3) на 2:
8a+4b=6 (5)

Теперь вычтем уравнение (5) из уравнения (3), чтобы исключить переменную b:
(4a+2b)-(8a+4b)=3-6
-4a=-3

Решим полученное уравнение для a:
a=(-3)/(-4)
a=3/4

Теперь, чтобы найти значение b, подставим найденное значение a в любое из исходных уравнений. Возьмем, например, уравнение (3):
4(3/4)+2b=3
3+2b=3
2b=0
b=0

Таким образом, мы получили значения переменных a=3/4, b=0 и c=2.

Итак, значение a равно 3/4.