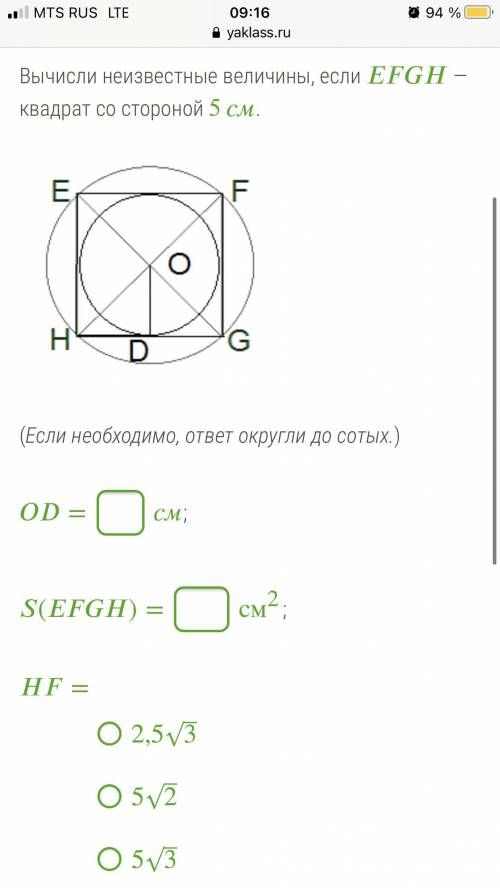
Вычисли неизвестные величины, если — квадрат со стороной 5 см

Для решения этой задачи, мы можем использовать основные принципы геометрии и свойства квадратов.

Первым шагом, давайте разберемся с данными. Нам дан квадрат со стороной 5 см.

Согласно свойствам квадрата, все его стороны равны. То есть, каждая сторона квадрата равна 5 см.

На изображении даны две величины, которые нам неизвестны. Давайте обозначим их как "a" и "b".

Воздушный шар находится внутри квадрата и касается его сторон. Поэтому, диаметр воздушного шара равен длине стороны квадрата. В данном случае, диаметр равен 5 см.

Диаметр шара также является диагональю квадрата. Рассмотрим треугольник, образованный диагональю квадрата и стороной, которую мы обозначаем как "a".

Мы знаем, что треугольник является прямоугольным, так как он образован диагональю и одной стороной квадрата.

Поэтому, мы можем использовать теорему Пифагора, которая гласит: в квадрате гипотенузы (самой длинной стороны прямоугольного треугольника) равна сумма квадратов катетов (двух других сторон).

Применяя данную теорему к нашему треугольнику, мы получим следующее уравнение:

a^2 + a^2 = 5^2

Решим это уравнение:
2a^2 = 25
a^2 = 25/2
a = √(25/2)
a = 5/√2
a = 5√2/2.

Теперь, рассмотрим треугольник, образованный диагональю квадрата и второй стороной "b".

Мы можем использовать ту же самую теорему Пифагора для этого треугольника:

b^2 + b^2 = 5^2

Решим это уравнение:
2b^2 = 25
b^2 = 25/2
b = √(25/2)
b = 5/√2
b = 5√2/2.

Таким образом, неизвестные величины "a" и "b" равны 5√2/2.

Я надеюсь, что это пояснение помогло вам понять, как я пришел к этому ответу. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их!