Вычеслите sin a/2 если sin a=4/5, 90<a<180
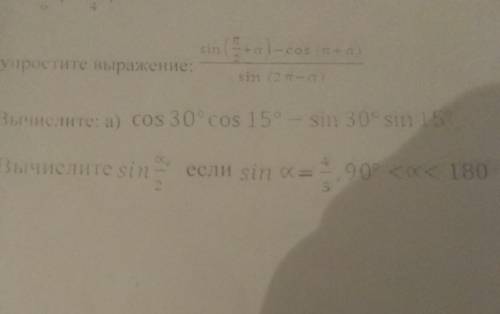
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите уравнение a2 - 16 / 5a2 - 20a при a = 0.4...
2 - Точка d (3, 16, -4) - середина отрезка bc. определите координаты точки...
3 - В1611 г.польский король сигизмунд 3 1)вторгся в россию 2)заявил о своем...
2 - Определить общее грамматическое значение каждого слова. мы отлично знаем,...
3 - Найти точки экстремума функции (мин ,макс) f(x)=2x^3-1/2x^4...
1 - Решите уравение: 1/x + 10/x^2+5x = x+3/5+x...
2 - Рассказ с обособленными и уточняющими словами, которые в тексте надо...
2 - Яка різниця потенціалів між точками поля якщо електрон маючи швидкість...
3 - Магнитная сила, действующая на горизонтально расположенный проводник,...
3 - Установите соответствие между странами, отмеченными на контурной карте,...
3
Объяснение:
=(cosa+cosa) /-sina=-2cosa /sina=-2ctga
sin(a/2) = √((1 - cos(a))/2)
Сначала нам нужно найти cos(a). Для этого воспользуемся тождеством: sin²(a) + cos²(a) = 1. По условию, sin(a) = 4/5, поэтому:
cos²(a) = 1 - sin²(a) = 1 - (4/5)² = 1 - 16/25 = 9/25
Теперь, найдя cos(a), мы можем вычислить sin(a/2):
sin(a/2) = √((1 - cos(a))/2)
= √((1 - 9/25)/2)
= √((25/25 - 9/25)/2)
= √(16/25 * 1/2)
= √(16/50)
= 4/√50
Оставив ответ в таком виде, мы его несколько упростили. Если потребуется, мы можем продолжить упрощение:
4/√50 = 4 * √(1/50) = 4 * √(1/25 * 1/2) = 4 * (1/5 * √(1/2)) = 4/5 * √(1/2)
Таким образом, sin(a/2) = 4/5 * √(1/2).