Вусеченном конусе радиусы оснований составляют 27см и 11см. образующая относится к высоте как 17: 15 . найдите объем полученного тела

Ответы

lerakuznyak 01.10.2020 06:59

Решение:

По условию, нам известно, что:

{образующая} : {высота} = 17 : 15.

Следовательно, мы можем сказать, что:

{образующая} = 17x

;{высота} = 15x

Дальше обратим внимание на то, что у нас образуется прямоугольный треугольник (на картинке ниже он выделен желтым).

А раз он прямоугольный, то для него будет верна теорема Пифагора (сумма квадратов катетов равна квадрату гипотенузы):

$(27-11)^2 + (15x)^2 = 17x^2\\\\16^2 + 225x^2 = 289x^2\\\\256 + 225x^2 = 289x^2\\\\64x^2 = 256\\\\x^2 = 4\\\\\left[\begin{array}{ccc}x_1=2\\x_2=-2\end{array}\right$

То, что мы возьмем только первый корень, вполне очевидно.

Теперь отвлечемся от теоремы Пифагора, и вспомним, как находить объем усеченного конуса:

$\boxed {V = \frac{1}{3} \cdot \pi \cdot h \cdot (R^2 + R \cdot r + r^2)}$

Что у нас есть:

$\pi \approx 3,14159...$ ; $h = 15x = 15 \cdot 2 = 30$ ; R = 27

;

Подставляем и считаем:

$\displaystyle V = \frac{1}{3} \cdot \pi \cdot 30 \cdot (27^2+27 \cdot 11 + 11^2)=10 \cdot \pi \cdot 1147 = 11470 \cdot \pi \approx \boxed {36 \; 034}$

В итоге - около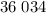 $36 \; 034$ см³.

ответ:

$\boxed { { 11 \; 470 \cdot {\pi }} }$ или около $\boxed {36 \; 034 \;\;\; cm^3}$ .

Вусеченном конусе радиусы оснований составляют 27см и 11см. образующая относится к высоте как 17: 15

ПОКАЗАТЬ ОТВЕТЫ

veros 01.10.2020 06:59

ответ:

11470·π (см³)

Объяснение:

Дано (см. рисунок у Olga8128 - всё в точности отражена):

В усеченном конусе

r = 11 см - радиус меньшего из оснований

R = 27 см - радиус большего из оснований

: h = 17 : 15 - отношение образующей к высоте

Найти: V - объем усеченного конуса.

Решение.

Пусть x коэффициент пропорциональности в отношении образующей к высоте. Тогда 17·x - длина образующей и 15·x - длина высоты.

Так как высота длиной 15·x, часть радиуса большего из оснований длиной 27-11=16 и образующая длиной 17·x образуют прямоугольный треугольник (на картинке ниже он выделен желтым), то отношение прилежащего катета к гипотенузе равен косинусу острого угла α между высотой и образующей:

$\displaystyle cos \alpha =\dfrac{h}{l} =\dfrac{15 \cdot x}{17 \cdot x}= \dfrac{15}{17}.$

Тогда синус острого угла α равен:

$\displaystyle sin\alpha =\sqrt{1-cos^{2}\alpha}= \sqrt{1-(\frac{15}{17} )^{2} }=\sqrt{1-\frac{225}{289} }=\\\\=\sqrt{\frac{289-225}{289} }=\sqrt{\frac{64}{289} }=\frac{8}{17}.$