Втреугольнике авс, заданном координатами вершин: а (7, 9), в (9, -6),
с (8, 10), найти уравнение и длину прямой, проходящей через точку с
параллельно стороне ав.

находим уравнение стороны AB:

A(7;9); B(9;-6)

уравнение прямой на плоскости через две точки:

Подставим координаты точек:

приведем уравнение к виду y=kx+b:

угловой коэффицент данной прямой:

k=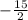

Если у прямых равны угловые коэффициенты, то они параллельны.

Составляем уравнение прямой с угловым коэффициентом k=-15/2 и проходящую через точку C(8;10)

Находим уравнение стороны BC:

Находим точку пересечения прямых y+16x-138=0 и 2y+15x-140=0:

Прямая 2y+15x-140=0 пересекается с BC в точке C и параллельна стороне AB=>  эта прямая касается треугольника ABC в точке C, и ее длина в этом треугольнике равна нулю.

1) 2y+15x-140=0

2) L=0