Второй член прогрессии равен 9. сумма третьего и четвертого членов этой прогрессии равна 4 . найдите первый и третий её члены, если произведение первого и второго члена положительно.

Ответы

vladmakarchuk80 21.09.2020 16:45

По формуле n-го члена геометрической прогрессии: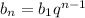 $b_n=b_1q^{n-1}$ :

$b_3+b_4=b_1q^2+b_1q^3=b_2q+b_2q^2=9q(1+q)=4\\ \\ 9q^2+9q-4=0$

Решая как квадратное уравнение, получим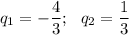 $q_1=-\dfrac{4}{3};~~ q_2=\dfrac{1}{3}$

Тогда: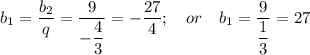 $b_1=\dfrac{b_2}{q}=\dfrac{9}{-\dfrac{4}{3}}=-\dfrac{27}{4};~~~or~~~ b_1=\dfrac{9}{\dfrac{1}{3}}=27$

Так как b1 * b2 = (-27/4) * 9 < 0, то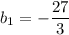 $b_1=-\dfrac{27}{3}$ отбрасываем. И так как 27*9 > 0, то удовлетворяет условию только b1 = 27 и знаменатель прогрессии q=1/3.

третий член: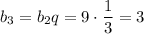 $b_3=b_2q=9\cdot\dfrac{1}{3}=3$

ответ: b1 = 27; b3 = 3.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

kurolesov71 29.04.2021 13:55

Выполните письменное задание...

хелпми23 29.04.2021 13:55

У столярній майстерні працюють майстер і його учень. За скільки днів учень може виготовити крісло, якщо він на виготовлення крісла витрачає на 3 дн(-ів, -я) більше, ніж...

Chcdhj 29.04.2021 13:55

Визнач квадрат суми одночленів 3х і 4у...

ghf8 29.04.2021 13:55

Найдите значение выражения: у²−8у+16у²−16 ÷10у−40у²+4у,при у=60 У меня сор по алгебре...

myzroman 28.07.2019 22:50

Представьте в виде многочлена 2-(3a-1)(a+5)...

tsibin1982 28.07.2019 22:50

Выполните действия. x^2-y^2/3x^2•6x/y^2+xy...

mot3333 28.07.2019 22:50

(8xy-5y+2)+(3y-3-8xy) преобразуйте в многочлен стандартного вида выражения...

ива357 28.07.2019 22:50

Найдите трехзначное натуральное число больше 650 но меньше 800 которое делится на каждую свою цифру и все цивры которого различны...

опшщапоащпощшап 28.07.2019 22:50

Выясните, имеет ли решения система и сколько: 5x-y=11 -10x+2y=-22...

dejavu1337 28.07.2019 22:50

Розкладить квадратне ривняня тричлена на множники (x-9)(x+4). (x+6)(x+1). (x+2)(x+3)...

Популярные вопросы