Всем ! напишите уравнение касательной к графику функции f(x)= 4x - 3x^2, проведённой в точке с абсциссой x0=2. заранее !

Ответы

superpuper90 10.06.2020 18:38

Общий вид уравнения касательной: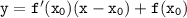 $\tt y=f'(x_0)(x-x_0)+f(x_0)$

1) Найдем значение функции в точке х0 = 2.

$\tt f(2)=4\cdot 2-3\cdot2^2=8-12=-4$

2) Производная функции: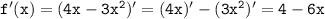 $\tt f'(x)=(4x-3x^2)'=(4x)'-(3x^2)'=4-6x$

Значение производной функции в точке х0 = 2:

$\tt f'(2)=4-6\cdot2=-8$

$\tt y=-8(x-2)-4=-8x+16-4=\boxed{\tt -8x+12}$ - уравнение касательной

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

alexey1009 17.04.2020 20:20

Colnkor 17.04.2020 18:37

[x^2]+x-42=0 Теорема Виета...

Ден2811 17.04.2020 18:37

erdgfgh 17.04.2020 18:38

alan001199 17.04.2020 18:40

Напишите основное свойство дроби...

veronichkastan123 17.04.2020 18:42

Известно, что а 5, b 4. Выбери верные утверждения...

AlumaZuma 17.04.2020 18:42

решить квадратным уравнением. 1 ВАРИАНТ А)...

Sonechka20052005 07.03.2021 02:54

StefaMusic2006 07.03.2021 02:07

яяяяяяяяяяяяяя22222 07.03.2021 02:05