Всё 19 и обязательно с решением

Другие вопросы по теме Алгебра
Популярные вопросы
- Мәтіннен берілген сөздердің баламасын (синоним) тауып жазыңыз a) жиналған –...
2 - написать сочинение на тему: «Мифологические персонажи в рассказе И.С. Тургенева...
3 - При разложении 52гр Сао выделился газ. Определите его объем...
1 - Задание 3 Как космос влияет на жизнь на земле? Приведи 1 пример....
2 - В зоопарке обезьяны ежедневно съедают 50 кг фруктов и овощей. Из них 20% бананов,...
2 - 7. Answer the questions. When do people get cards like this?When do you see...
1 - Write true sentence with have to. сейчас пряи нааадооо ...
3 - Задание: Единственный собрать весь уражай-этт двигаться вперед пока не доберешься...
1 - Определите роль данного эпизода в произведении Снегурочка . Для подтверждения...
2 - 2. Радиусы 3 см, 4 см, 5 см. О. Три круга с их центрами прилегают друг к другу....
3
В полученном интервале есть только одно целое число, равное 2 . Поэтому и сумма всех целых чисел из полученного промежутка равна 2 .
Объяснение:
а)![\left[\begin{array}{ccc}3x-5x-3\\2x+4x-2\end{array}\right]](/tpl/images/1700/0828/4f20c.png) ≡
≡ ![\left[\begin{array}{ccc}3x-x-3+5\\4-5x+2x\end{array}\right]](/tpl/images/1700/0828/1b795.png) ≡
≡ 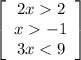 ≡
≡ 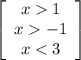
x ∈ ] 1; 3 [ корни "1" и "3" в интервал не входят, единственное целое число в данном интервале это "2"
решение первой системы расписал по подробнее, остальные конкретно не расписываю, но основные преобразования показаны.
б)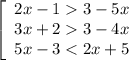 ≡
≡ 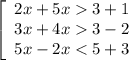 ≡
≡ 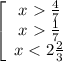
x ∈ ] ;
; 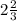 [ , целые числа в данном интервале это "1" и "2"
[ , целые числа в данном интервале это "1" и "2"
в)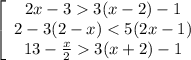 ≡
≡ 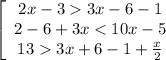 ≡
≡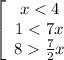 ≡
≡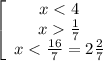
x ∈ ] ;
; 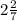 [ , целые числа в данном интервале это "1" и "2"
[ , целые числа в данном интервале это "1" и "2"
успехов