Впрямоугольнике авсd со сторонами ав=2, вс=5 случайно выбирают точку. найти вероятность того что она расположена ближе к вершине а, чем к точке пересечения диагоналей. с решением плз
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите элемент : 1.масса одного из стабильных изотопов которого...
1 - На какую из сторон горизонта указывает полярная звезда при ориентировании...
1 - Сказка чего на свете бывает какому виду она относится и над...
3 - Решите пропорцию 3 1/2х: 7 2/3 = 2 2/23 : 1 1/7...
3 - Подскажите! из данных слов выберите и вставте в предложение....
2 - Ссаша нашол 50 яблок саша разделил с машей по 5 яблок сколько...
1 - Розовые скворцы неутомимые путешественники по местам кормления...
3 - Решить. найдите числовое значение выражения, предварительно...
2 - Сочинение на тему образ стародума недоросль только не с интернета...
2 - Вмешке 7 кг пшена. как при чашечных весов и одной 200-граммовой...
1
Проведем серединный перпендикуляр к АО. Из прямоугольного треугольника ACD по теореме Пифагора
Треугольники AKM и ACD подобны по двум углам (∠AKM = ∠ADC и ∠А - общий).
AM/AK = AC/AD ⇒ AM=29/20
Треугольники AKM и NKC подобны по двум углам (∠AKM=∠CKN и ∠KAM = ∠NCK как накрест лежащие при BC || AD и секущей AC).
AM/AK = NC/CK = (BC-BN)/(AC-AK) ⇒ BN = 13/20
Площадь четырехугольника ABNM: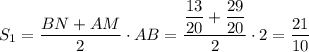
Площадь прямоугольника ABCD: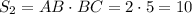
Искомая вероятность по геометрической формуле вероятности:
ответ: 0,21.