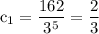Впрогрессии cn=54; q=3; sn=80 2/3. найти с1 и n.
Другие вопросы по теме Алгебра
Популярные вопросы
- Росту (не)знакомец был (не)высокого и (не)низкого ,в плечах широко...
2 - Фонетический разбор слова жуют зарание...
1 - Краствору серной кислоты массой 250 г с массовой долей h2so4 равной...
3 - Вкакой координатной четверти расположен угол альфа, если: 1) sinа...
1 - Почему камертон укрепляют на деревянном ящике?...
1 - Вычислите число молекул,которое содержится в стакане воды объемом...
1 - 14. политический режим, которому присущи такие характеристики, как...
1 - 1)в треугольнике abc угол c равен 60 градусов, угол b равен 82 градуса....
3 - Концессия это: а) возможность после выполнения государственного заказа...
1 - Замените зависимое слово антонимом. лёгкий портфель,лёгкий мороз,лёгкий...
1
Из формулы n-го члена геометрической прогрессии:
Выразим первый член этой прогрессии:
Подставим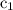 в сумму, получим
в сумму, получим
Первый член геом. прогрессии: