Восновании прямой призмы abca1b1c1 лежит прямоугольный треугольник авс (угол c=90 градусов), ac=4см, bc=3см. через сторону ac и вершину b1 проведена плоскость, угол b1ac=60 градусов. найдите площадь боковой поверхности призмы.

Из треугольника ABC по т. Пифагора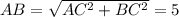 см.

Так как BB₁ ⊥ (ABC) и BC ⊥ AC то B₁C ⊥ AC (по теореме о трех перпендикулярах), следовательно, ΔB₁CA - прямоугольный.

∠B₁AC = 60°, тогда ∠AB₁C = 90° - 60° = 30°

Против угла 30° гипотенуза АВ₁ в два раза больше катета АС,т.е.

AB₁ = 2AC = 2 * 4 = 8 см

Из прямоугольного треугольника AB₁B: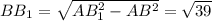 см

Площадь боковой поверхности призмы:

 Sбок = Pосн * h = (AB+BC+AC)*BB₁ = (5+3+4)*√39 = 12√39 см²

ответ: 12√39 см²