1. Алгебра
  2. Вопрос по тригонометрии. Имеем

Вопрос по тригонометрии. Имеем уравнение : 4sin^2x = tgx Заменим tgx 4sin^2x = sinx / cosx Вопрос: Почему нельзя сделать так - 4sin^2x = sinx / cosx | *cosx 4sin^2x * cosx= sinx | : sinx (4sin^2x * cosx) / sinx = 0 4sinx*cosx = 0 | :4 И получается две серии корней sinx=0 или cosx=0 В чём ошибка? Почему так нельзя делать?

lolisgd lolisgd    3   17.06.2020 17:27    0

Ответы
norucov norucov  15.10.2020 14:18

4\sin^2x = \mathrm{tg}x

Тангенс определен при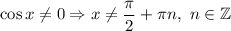 \cos x\neq 0\Rightarrow x\neq \dfrac{\pi}{2}+\pi n,\ n\in\mathbb{Z}

4\sin^2x - \mathrm{tg}x=0

4\sin^2x - \dfrac{\sin x}{\cos x} =0

\sin x\left(4\sin x - \dfrac{1}{\cos x} \right)=0

\sin x\cdot \dfrac{4\sin x\cos x-1}{\cos x} =0

\sin x\cdot \dfrac{2\sin 2x-1}{\cos x} =0

\left[\begin{array}{l} \sin x =0\\ 2\sin 2x-1=0\end{array}

\left[\begin{array}{l} \sin x =0\\ \sin 2x=\dfrac{1}{2}\end{array}

\left[\begin{array}{l} x =\pi n \\ 2x=(-1)^k\dfrac{\pi}{6}+\pi k\end{array}

\left[\begin{array}{l} x =\pi n,\ n\in\mathbb{Z}\\ x=(-1)^k\dfrac{\pi}{12}+\dfrac{\pi k}{2} ,\ k\in\mathbb{Z}\end{array}

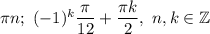
ответ: \pi n;\ (-1)^k\dfrac{\pi}{12}+\dfrac{\pi k}{2},\ n, k\in\mathbb{Z}

По поводу предлагаемого решения: домножить на cosx можно, поскольку это выражение не может быть нулевым. А вот разделить на sinx просто так нельзя, потому что мы потеряем корни. Когда мы делим на некоторое выражение, мы полагаем что оно не равно нулю. Но здесь при подстановке sinx=0 в исходное уравнение мы получаем верное равенство. И, наконец, еще: вообще при делении sinx на sinx получается 1, а не 0, но мы уже выяснили, что этого вовсе делать не надо.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
LLA7A LLA7A  15.03.2019 11:50
Постройте график функции y=-2x-4. укажите с графика при каком значении аргумента значение функции равно 2...
antonareninozvuw8 antonareninozvuw8  15.03.2019 11:50
Каково взаимное расположение графиков функций y=15x-51 и y=-15x+39? обьясните ответ . в случае пересечения графиков найдите координаты их точки пересечения...
вованн2 вованн2  15.03.2019 11:50
Плз )) 1) найдите наименьшее целое решение неравенства \\ - это дробная черта 2х+2\\5 - х-1\\2 2 2,3,4 - решите уравнение 2) 3y+9\\5 + 5y - 5\\4 = 6 + 3y+1\\2 3) x+9\\7...
2мария3 2мария3  15.03.2019 11:50
Ab под корнем(а под корнем+b под корнем равно ? ?...
Thfhgdrhd Thfhgdrhd  15.03.2019 11:50
(5х - 10х/х+1) поделить на 15х - 15/4х+4 / - дробь;...
marusja82 marusja82  15.03.2019 11:50
Сократить пример по максимуму, заранее за *_* (а+3/а-3 + а-3/а+3) поделить на 3а^2+27/9-а^2 / - знак дроби; ^2 - квадрат числа;...
настёна55556566666 настёна55556566666  15.03.2019 11:40
Решите , выделяя три этапа моделирования: 1. гипотенуза прямоугольного треугольника равна 17 см, а периметр треугольника равен 40 см. найти катеты прямоугольного треугольника....
Darya4567 Darya4567  15.03.2019 11:40
Найдите все значения а при которых неравенство (а+4)х²-2ах+2а-6 0 выполняется, х€r...
annatarasova1991 annatarasova1991  15.03.2019 11:40
Вурне 9 белых и 6 черных шаров .из урны вынимают два шара.какова вероятность того,что оба шара окажутся белыми? ?...
feroprosto feroprosto  15.03.2019 11:40
Найдите все простые числа,на которые делится сумма любых четырех последовательных степеней часла 2...

Популярные вопросы