1. Алгебра
  2. Вобщем решить и разжевать мне,

Вобщем решить и разжевать мне, что и как у вас получилось, буду . ничего не понимаю про эти линейные уравнения. ​

vika78678 vika78678    2   11.11.2019 20:44    1

Ответы
KatyshaMarina KatyshaMarina  10.10.2020 12:32

Нам нужно составить линейную систему уравнений вида

$\left \{ {{a\cdot x+b\cdot y=e} \atop {c\cdot x+d\cdot y=f}} \right.

Вместо коэффициентов a,b,c,d подставляем какие-то числа, которые нам в голову придут, чтобы вычислить e и f подставим ещё x,y из задания

a)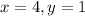 x=4, y=1

Пусть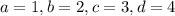 a=1,b=2,c=3,d=4

1\cdot 4 +2\cdot 1=6=e;\\ 3\cdot 4+4\cdot 1 =16=f;

Получаем систему

$\left \{ {{x+2y=6} \atop {3x+4y=16}} \right.

Решим её

$\left \{ {{x=6-2y} \atop {3(6-2y)+4y=16}} \right.\Rightarrow \left \{ {{x=6-2y} \atop {18-6y+4y=16}} \right. \Rightarrow \left \{ {{x=6-2y} \atop {2y=2}} \right. \Rightarrow \left \{ {{x=4} \atop {y=1}} \right.

Решение действительно как в задании, значит, все верно сделано.

Аналогично со второй системой

б) пусть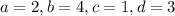 a=2,b=4, c=1,d=3

2\cdot 0+4\cdot 3 = 12=e\\ 1\cdot 0+3\cdot 3 = 9 = f

Система:

$\left \{ {{2x+4y=12} \atop {x+3y=9}} \right. \Rightarrow \left \{ {{2(9-3y)+4y=12} \atop {x=9-3y}} \right.\Rightarrow \left \{ {{18-6y+4y=12} \atop {x=9-3y}} \right.

$\Rightarrow \left \{ {{2y=6} \atop {x=9-3y}} \right. \Rightarrow \left \{ {{y=3} \atop {x=0}} \right.

Решение совпадает с тем, что указано в задании, все верно.

P.S. по поводу придумывания коэффициентов.

1. Они не должны быть все нулевые

2. Любое из двух уравнений системы не должно выводиться из другого уравнения системы. Пример:

$\left \{ {{x+y=5 } \atop {2x+2y=10}} \right.

Видно, что второе уравнение - первое уравнение, умноженное на 2. Такого тоже не должно быть. Вообще такие уравнения являются линейно зависимыми.

То есть не все числа подойдут, небольшое ограничение есть)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Anotherdream Anotherdream  05.05.2019 16:59
Питання для диктанту (2 травня) «системи лінійних рівнянь з двома змінними» 1. що називають розв язком рівняння з двома змінними? 2. що означає розв язати рівняння з двома змінними?...
Alips Alips  05.05.2019 16:55
Представьте в виде многочлена в стандартном виде: (3n-2) ∙ (4n+1). заранее !...
maria2005dp maria2005dp  05.05.2019 16:54
Сократите дробь, необходимо решение....
viliam3486 viliam3486  05.05.2019 16:50
Решите показательное уравнение 0,5^х²-5х 16²х...
MeerDasha487 MeerDasha487  05.05.2019 16:49
Нужны формулы для решения тригонометрических уравнений (общие и частные случаи)...
olesiadukova olesiadukova  05.05.2019 16:48
Известно, что зажигалка не срабатывает в 1 случае из 20. найти: а) вероятность того, что из 5-и зажиганий она сработает больше половины раз; б) наиболее вероятное количество несрабатываний...
Sanchos106 Sanchos106  05.05.2019 16:47
Решите , надеюсь всё будет правильно. 35...
Клубничка0987654322 Клубничка0987654322  05.05.2019 16:47
Впервой ёмкости на 5 л жидкости больше, чем во второй. если из первой ёмкости перелить во вторую 14 л жидкости, то во второй ёмкости станет в 2 раза больше, чем останется в первой....
дэнчик60 дэнчик60  05.05.2019 16:47
Преобразовать выражение. с подробным решением. не моё! ​...
Nna564 Nna564  31.01.2022 13:28
4.Решите уравнение: (2y-3)(3y+1)+2(y-5)=2(1-2y)^2+6y...

Популярные вопросы