Во всех заданиях напишите подробное решение Задание 1
Докажите тождество:
Задание 2
Упростите выражение:
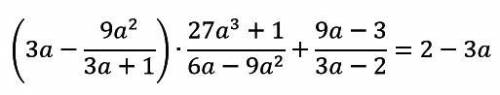
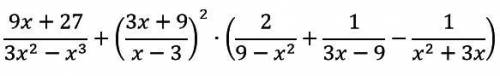
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое суждение верно характеризует взаимовлияние биологической природы и социальной...
2 - Хто навчив Михайлика читати?(Гусі лебеді летять)...
1 - іі. Обчислити масу етилену , яку можна добути з етанолу масою 5,6 кг, якщо масова...
1 - надо! Сочинение на тему подруга дней моих суровых...
2 - Готичний стиль витіснив романський?...
1 - Как называется свойство выражаемое равенством (ab)c= a(bc)? Выберите один из 4...
2 - Допиши окончания глаголов. Подпиши спряжение: Он сверка_т( ) , она кос_т( ), ты...
3 - выпишите 3 примера предложений из «Капитанской дочки»: называемые, определенно...
3 - Уровень А (оценка 3 ) не требует развернутого решения (необходимо только отметить...
3 - Периметр прямоугольника 48см, а его площадь 23см^2. Найдите меньшую сторону прямоугольника...
3
Что и требовалось доказать