Внутри клетчатого прямоугольника закрашено несколько клеток, образующих квадрат. Оказалось, что закрашенные клетки есть в 20 % строк и в 45 % столбцов. Из скольких клеток может состоять такой прямоугольник?
Варианты (А) 1800 (Б) 900 (В) 450 (Г) 300 (Д) 100

Ответы

kseniyes5454 11.10.2020 21:57

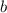Пусть прямоугольник содержит строк и столбцов. Найдем его площадь:

S=ab

По смыслу задачи это искомое число клеток прямоугольника. Обозначим его буквой М, где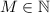 $M\in\mathbb{N}$ :

M=ab

Закрашенные ячейки содержат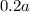 0.2a строк и 0.45b столбцов. Найдем площадь закрашенной области:

$S_0=0.2a\cdot0.45b=0.09ab$

S_0=0.09M

Но закрашенная область - это квадрат. Найдем его сторону:

$a_0=\sqrt{S_0} =\sqrt{0.09M}=0.3\sqrt{M}$

Полученное число соответствует некоторому количеству клеток, а значит должно быть натуральным:

$0.3\sqrt{M}\in\mathbb{N}$

Кроме этого, число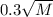 $0.3\sqrt{M}$ составляет 20 % и 45 % от натуральных чисел, выражающих количество строк и столбцов в исходном прямоугольнике. то есть:

$\left(0.3\sqrt{M}:0.2\right)\in\mathbb{N}$

$\left(0.3\sqrt{M}:0.45\right)\in\mathbb{N}$

Преобразуем числа:

$0.3\sqrt{M}:0.2=0.3\sqrt{M}:\dfrac{1}{5} =5\cdot0.3\sqrt{M}$

$0.3\sqrt{M}:0.45=\dfrac{3}{10} \sqrt{M}:\dfrac{9}{20} =\dfrac{3}{10} \cdot\dfrac{20}{9}\sqrt{M}=\dfrac{2}{3}\sqrt{M}$

Заметим, что первое условие выполняется при ранее поставленном условии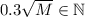 $0.3\sqrt{M}\in\mathbb{N}$ , поэтому его далее учитывать не будем.

Таким образом должно выполниться два условия:

$\begin{cases} 0.3\sqrt{M}\in\mathbb{N} \\ \dfrac{2}{3}\sqrt{M}\in\mathbb{N}\end{cases}$

Эти условия можно объединить в одно.

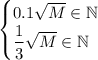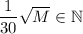Если выполнятся условия $\begin{cases} 0.1\sqrt{M}\in\mathbb{N} \\ \dfrac{1}{3}\sqrt{M}\in\mathbb{N}\end{cases}$ , то и предыдущие условия будут верны. А для проверки этих условий достаточно проверить, что $\dfrac{1}{30}\sqrt{M}\in\mathbb{N}$ .