ВНИМАНИЕ Решите пошагово, с подробным описанием действий. Без воды.
Log X по основанию 2 = 3
Log27 по основанию x = 3
Log (x^2 - 1) по основанию 3 = 1
3^x > 5
Другие вопросы по теме Алгебра
Популярные вопросы
- Березовая роща ответить на вапрос чему учит сказка...
2 - 5 activate prepare a new dialogue with a partner. use situation 1. practise...
1 - Только разбавленная серная кислота реагирует со всеми веществами ряда:1...
3 - Прочитай текст и изобрази семейное дерево, включающее всех перечисленных...
3 - На клетчатой бумаге нарисована таблица 5 x 6. У Васи есть неограниченный...
2 - Знайдіть частку : 2 1/2 * 1 3/4...
1 - Сосредоточьтесь на произведении искусства и ответьте на вопросы...
2 - Упражнение 16. Согласуйте определения с несклоняемыми существительными....
2 - H2SO4(разбавленная) + BaCl2 = ? (+ионная форма)...
1 - Үй тапсырмасы 4. Қазақтың дәстүрлі ән жанры мен қазақтың опера жанрының...
2
Логарифм - показатель степени, в которую нужно возвести основание, чтобы получить число под знаком логарифма.
По определению логарифма получаем, что
Аналогично по определению логарифма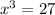 , откуда
, откуда 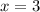 .
.
Прологарифмируем обе части по основанию 3:
По свойствам логарифмов степень числа под знаком логарифма можно вынести за логарифм:
Поскольку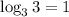 , получаем:
, получаем: