Внесите множители под знак корня, если a>0 и b>0. Если что перед выражением стоит "-"
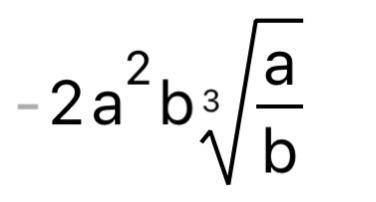
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему изучение компьютерных операционных систем актуальна...
2 - Решите уравнение x²+x-2 и делить на x+2 дробь...
3 - Какие окончания у первого склонения...
1 - 1)вычислите след. примеры в двоичной системе счисления 1101100000₂...
1 - Что изображали первобытные художники?...
3 - Верно ли что: 1)12 называют делителем числа 4? 2)12 называют...
2 - Найдите значение a по формуле а=4b-16 при b=8 .. нужно !...
2 - Склади й запиши опи калини (3-4реченя...
1 - Информационное сообщение объемом 240 битов состоит из 80 символов....
3 - Вкаком словосочетание неверно указано главное слово 1) быстро...
3
Смотри.......................
Выражение на картинке содержит два множителя: √(a^2 * b^3). Чтобы внести множители под знак корня, мы разбиваем выражение на две части: корень из a^2 и корень из b^3.
Первый множитель: √(a^2). Для того чтобы извлечь корень из квадрата a, мы должны применить математическое свойство корня: √(a^2) = a. Таким образом, первый множитель равен a.
Второй множитель: √(b^3). В этом случае у нас есть степень тройки внутри корня. Здесь мы можем использовать свойство корня, которое гласит, что корень из произведения равен произведению корней: √(b^3) = √(b^2 * b). Затем мы можем разбить этот корень на два корня: √(b^2) * √(b).
Первый корень √(b^2) равен b, так как мы извлекаем корень из квадрата b. Второй корень остается неизменным: √(b). Таким образом, второй множитель равен b * √(b).
Собирая все вместе, наше выражение будет выглядеть следующим образом: -a * b * √(b).
Таким образом, множители под знаком корня будут a и b, итоговый ответ -a * b * √(b).