Внесите множитель под знак корня 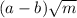
если а<b,
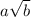
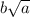
Другие вопросы по теме Алгебра
Популярные вопросы
- (35+63)-21-(16+8)= как правильно решать?...
3 - Дополини сложные предложения к предложению: наступила весна,...
1 - Разбор по составу слов словарный кормушка книга...
3 - Напишите решение : а) 5% от 300, б) 6% от 700...
2 - Отметь слово,в котором третий звук-непарный мягкий,глухой согласный: а.озёра....
3 - 137см5мм+18см2мм.1827см2мм-29см3мм.450м3дм+729м7дм....
1 - Составьте список ключевых слов для текста,в котором нужно рассказать о...
1 - Сделайте всё правильно плз : d 9,10...
3 - Вчём проявлялась централизация франции?...
3 - Доклад про рене декарт кем он был ? какие открытия совершил?...
2
1.
Если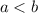 , то
, то 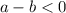 . Но внести под знак корня мы можем только неотрицательный множитель. Тогда, преобразуем следующим образом:
. Но внести под знак корня мы можем только неотрицательный множитель. Тогда, преобразуем следующим образом:
2.
Аналогично, необходимо рассмотреть два случая:
3.
Уточнение. Если условие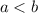 относится и к двум последним примерам тоже, то для второго примера оно не никак. А для третьего примера на основе него можно сделать вывод, что множитель перед корнем больше числа, стоящего под знаком корня. Но поскольку под корнем стоит заведомо неотрицательное число, то и множитель перед корнем также неотрицателен. Тогда однозначно
относится и к двум последним примерам тоже, то для второго примера оно не никак. А для третьего примера на основе него можно сделать вывод, что множитель перед корнем больше числа, стоящего под знаком корня. Но поскольку под корнем стоит заведомо неотрицательное число, то и множитель перед корнем также неотрицателен. Тогда однозначно 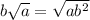 .
.