Влаборатории производится анализ крови. содержание сахара в крови вычисляется как среднее арифметическое результатов нескольких из- мерений. таблица содержит результаты пяти измерений содержания сахара (г/л) в одной пробе крови взрослого пациента. номер измерения 1 2 3 4 5 содержание сахара (г/л) 120 180 110 90 100 а) найдите среднее арифметическое результатов измерений; б) найдите дисперсию результатов измерений. выбрано правило: если квадрат отклонения значения от среднего арифме- тического превышает дисперсию больше чем в 3,5 раза, то это значение счи- тается ненадежным (выбросом) и в дальнейшем не учитывается. в) определите, является ли значение 180 ненадежным в соответствии с вы- бранным правилом. г) найдите среднее арифметическое всех надежных значений. д) нормальное содержание сахара в крови взрослого 80–110 г/л. можно ли считать, что у данного пациента нормальное содержание сахара в крови?

Ответы

Анжела1411 01.10.2020 01:54

а)среднее арифметическое равно:

(120+180+110+90+100)/5=600/5=120.

б)Сначало рассчитаем отклонение от нормы.

1. 120-120=0

2. 180-120=60

3. 110-120=-10

4. 90-120=-30

5. 100-120=-20

Дисперсия обозначим её d(Дисперсия множества из N членов находится путем сложения квадратов их отклонений от среднего значения и деления на N).

$d=\frac{(0)^2+(60)^2+(-10)^2+(-30)^2+(-20)^2}{5}=\frac{3600+100+900+400}{5}=\frac{5000}{5}=\\=1000$

в)Отклонение от значения 60, дисперсия 1000. Исходя из правила получаем.

$\frac{60^2}{1000}=\frac{3600}{1000}=3.6$

Т.к. 3.6>3.5 то значение 180 ненадёжное(выброс)

г)1.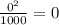 $\frac{0^2}{1000}=0$ - надёжное.

2.Ненадёжное. Находили выше.

3.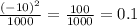 $\frac{(-10)^2}{1000}=\frac{100}{1000}=0.1$ - надёжное.

4.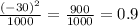 $\frac{(-30)^2}{1000}=\frac{900}{1000}=0.9$ - надёжное.

5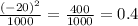 $\frac{(-20)^2}{1000}=\frac{400}{1000}=0.4$ - надёжное.

Впринципе можно было и не проверять, оно и так понятно)))

$\frac{120+110+90+100}{4}=\frac{420}{4}=105$

д) Да,т.к. значение 180 мы не учитываем. А среднее арифметическое 4 значение равно 105.

Вродебы так если нигде не ошибся)))

ПОКАЗАТЬ ОТВЕТЫ

Катядонецк 10.01.2024 09:48

а) Сначала найдем среднее арифметическое результатов измерений. Для этого нужно сложить все результаты и разделить сумму на количество измерений:

120 + 180 + 110 + 90 + 100 = 600 (сумма результатов)
600 / 5 = 120 (среднее арифметическое)

Ответ: среднее арифметическое результатов измерений равно 120.

б) Чтобы найти дисперсию, нужно вычислить сумму квадратов разностей каждого значения от среднего арифметического, а затем разделить эту сумму на количество измерений:

(120 - 120)^2 + (180 - 120)^2 + (110 - 120)^2 + (90 - 120)^2 + (100 - 120)^2 = 0 + 3600 + 100 + 900 + 400 = 5000 (сумма квадратов разностей)
5000 / 5 = 1000 (дисперсия)

Ответ: дисперсия результатов измерений равна 1000.

в) Теперь проверим, является ли значение 180 ненадежным, используя выбранное правило. Для этого найдем квадрат отклонения значения 180 от среднего арифметического и сравним его с дисперсией, умноженной на 3,5:

(180 - 120)^2 = 3600 (квадрат отклонения значения 180 от среднего арифметического)
1000 * 3,5 = 3500 (дисперсия, умноженная на 3,5)

Так как квадрат отклонения значения 180 превышает дисперсию больше, чем в 3,5 раза, то это значение считается ненадежным.

Ответ: значение 180 является ненадежным.

г) Теперь найдем среднее арифметическое всех надежных значений. Для этого нужно исключить ненадежное значение и посчитать среднее арифметическое оставшихся надежных значений (120, 110, 90 и 100):

(120 + 110 + 90 + 100) / 4 = 420 / 4 = 105

Ответ: среднее арифметическое всех надежных значений равно 105.

д) Нормальное содержание сахара в крови взрослого составляет 80–110 г/л. Для того, чтобы считать, что у данного пациента содержание сахара в крови нормальное, его среднее арифметическое должно быть в этом диапазоне.

Так как среднее арифметическое всех надежных значений равно 105 г/л, и это значение находится в диапазоне нормального содержания сахара в крови, то можно считать, что у данного пациента нормальное содержание сахара в крови.

Ответ: у данного пациента можно считать, что содержание сахара в крови является нормальным.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра