Вирішіть, будь ласка, це рівняння та наступне:
{x⁴+x²y²=20
{y⁴+x²y²=5
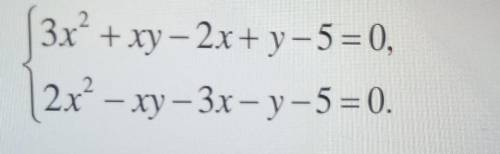
Другие вопросы по теме Алгебра
Популярные вопросы
- В чëм отличие системы образования в России 18 века и образования...
2 - На рисунке изображен график движения всадника. Рассмотрев график,...
1 - 12.Государство, разработавшее корабль-небоскреб, для изучения океанов...
1 - ЗАДАНИЯ Мәтінді мұқият оқып, төмендегі тапсырмаларды орындаңыз.Кең...
1 - Знайти інтервали монотонності та точки екстремума функц )...
1 - Жаңа технология жетістіктері Күнделікті өмірде қандай жаңа техникаларды...
1 - Написать 5 видов вопросов к предложению I love being involved in...
1 - С Красивыми чертами лица, кудрявыми белокурыми волосами, светлыми...
2 - Укажите род и жанр к которому относится произведение Лермонтова...
2 - Объясните, как вы понимаете термины «инициация» и «трансмиссия»...
3
Первое (фотография):
3х^2+ху-2х+у-5=0
+
2х^2-ху-3х-у-5=0
=
5х^2-5х-10=0 |:5
х^2-х-2=0
D= (-1)^2-4×1×(-2)
D= 9
X1= (1-3)/2 = -1
X1= (1-3)/2 = -1X2= (1+3)/2 = 2
2) Подставляем Х1 в любое из начальных уравнений, и находим у1:
3(-1)^2+(-1)×у-2(-1)+у-5=0
3-у+2+у-5=0
-у+у=5-5
0=0 (верно, следовательно У принадлежит от минус бесконечности до плюс бесконечности (R))
3) Подставляем Х2 в любое из начальных уравнений и находим у2:
3(2)^2+2у-2×2+у-5=0
12+2у-4+у-5=0
3+3у=0
3у= -3 |:3
у= -1
ответ: при х1=-1,у=R; (2;-1)
Вторая система:
{x⁴+x²y²=20
+
{y⁴+x²y²=5
=
х^4+у^4+2х^2у^2=25
(х^2+y^2)^2=25, следовательно
x^2+y^2=5
x^2=5-y^2
Подставим во второе уравнение:
у^4+5у^2-у^4=5
5у^2=5 |:5
у^2=1
у1=1
у2= -1
Подставим у1 и у2 в x^2=5-y^2:
1) х^2= 5-1^2
х^2=4
х1=2
х2= -2
2) х^2=5-(-1)^2
х^2=4
х1=2
х2=-2
ответ: (2;1); (-2;1); (2;-1); (-2;-1).