Вчём суть доказательства от противного? ,

Мы делаем предположение, что то, что нам дано неверно, к примеру:

Доказать иррациональность числа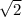

Допускаем противное, что число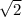 - рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:

Любое рациональное число можно представить как несократимую дробь, где числитель - целое число, а знаменатель - натуральное

Отсюда следует, что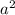 чётно, значит, чётно и a; следовательно, 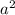делится на 4, а значит, 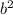и 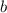тоже чётны. Полученное утверждение противоречит несократимости дроби 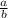. Это противоречит изначальному предположению и 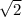- иррациональное число.