Варифметической прогрессии сумма первого и девятого членов равна 64. найдите разность между суммой ее девяти первых членов и пятым членом прогрессии?
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.Две бригады,работая вместе,могут отремонтировать дорогу за...
3 - В природе встречаются 4 изотопа серы: 32S, 33S, 34S, 36S. Определите...
2 - Запиши рядом с данными названиями слоёв кожи буквы, соответствующие...
3 - 1.Территория национально-освободительного восстания казахов...
2 - [1] 3. Внимательно прочтите текст. Заполните схему составления...
3 - 1) Приведите 2 аргумента в пользу этого суждения и 2 аргумента...
2 - Теңдеуді шеш:5(х-2)-6=4+3(х-2)...
3 - Напишите уравнения реакций 3,4-диметилгексан + Cl2=Изобутан...
1 - Электрическое поле образовано двумя неподвижными вертикально...
2 - Определите режим работы гироскапического датчика с камандным...
1
Мы знаем свойство арифметической прогрессии: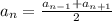 . По сути оно доказывается тем, что
. По сути оно доказывается тем, что 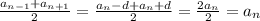 . И если каждое из d домножить на какое-то натуральное число x, то они всё равно взаимоуничтожатся:
. И если каждое из d домножить на какое-то натуральное число x, то они всё равно взаимоуничтожатся: 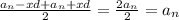 . Но
. Но 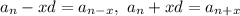 . То есть это свойство можно записать так:
. То есть это свойство можно записать так: 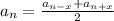 .
.
Именно такая ситуация в этой задаче: 5 стоит посередине между 1 и 9 (5-4 = 1, 5+4 = 9). Применим полученное свойство:
Сумма первых девяти членов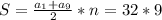
Тогда искомая разность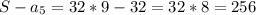
ответ: 256
Объяснение:
(Распишем расчёт чтоб было легче)
а1+а9 64
а5= = =32
2 2
a5=32
S-а =32*9-32=256
5