Варианте найти общий интеграл дифференциального уравнения:
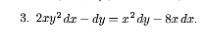
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите жанровые признаки басни любопытный...
3 - определить степень окисления....
3 - 1/10 см сколько миллиметров? без обмана, если с обманом то вы тогда эгоисты...
3 - Чоловік з резус-негативною 1 групою крові (гомозигота) одружився з жінкою, що має...
1 - Знайдіть ємність плоского повітряного конденсатора, якщо площа кожної його пластини...
1 - ответьте на любой из двух вопросов, если можете сразу на два вопросана первый вопрос...
3 - Ашық райға мысал патом бұйрық райы 2 сөйлемнен...
1 - 3. берілген уақыт бөлшем бірліктерін ұзақтығынабайланысты кему ретімен жазыңыз.апта,...
2 - Представьте , если это возможно, число в виде десятичной дробей : 1,5/6 ; 9/20;...
3 - Antworte auf die fragen. необходимо ответить на вопросы, написав словами, что изображено...
2
общее решение