ів. ЗА ВІДПОВІДЬ НЕ В ТЕМУ — ВИДАЛЯЮ
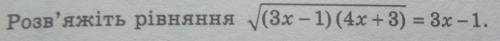
Другие вопросы по теме Алгебра
Популярные вопросы
- Выпиши имена существительные среднего рода.обозначь их окончания...
2 - Ломаной из трёх звеньев раздели прямоугольник на 4 одинаковых многоугольника...
2 - Алгоритм деления столбиком 455: 13,688: 16,528: 22,345: 15,4656:...
2 - Найти наречия в пословице. дальше земли не упадешь...
3 - Бак вмещает в 7 раз больше воды чем 5ведер.сколько литров воды...
2 - Масса сушеных грибов составляет одну 10-ю часть массы свежих грибов...
1 - Мыналарга тең болатын сандарды жаз; 3онд.5бірлік пен 4онд косындысына...
3 - Корень из трёх в 3 степени умножить на корень из 48=...
3 - Правила рационального поведения потребителя...
3 - Найдите высоту равнобокой трапеции основание которой 10 и 8 см....
2
√(3x - 1)(4x + 3) = 3x - 1
ограничения
(3x - 1)(4x + 3) ≥ 0 как подкоренное выражение корня четной степени корня (одз)
3х - 1 ≥ 0 х≥ 1/3 как выражение корня четной степени (неотрицательно)
так как оба вырадения >= 0 в квадрат
(3x - 1)(4x + 3) = (3x - 1)²
(3x - 1)² - (3x - 1)(4x + 3) = 0
(3x - 1)(3x - 1 - (4x + 3)) = 0
(3x - 1)(x + 4) = 0
x = -4 не корень x ≥ 1/3
x = 1/3 корень
ответ 1/3
Відповідь:
Пояснення: