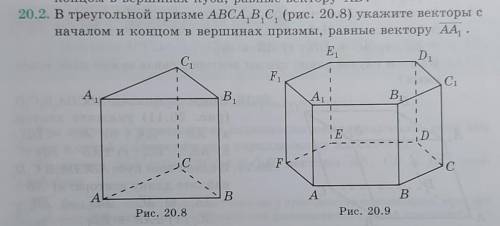
В треугольной призме ABCA,B,C, (рис. 20.8) укажите векторы с началом и концом в вершинах призмы, равные вектору АА, .

​

Для решения данной задачи, нам необходимо найти векторы, которые соответствуют отрезку АА, в треугольной призме ABCA,B,C.

Для начала, давайте определим координаты вершин треугольной призмы ABCA,B,C. По рисунку, мы видим, что вершина A имеет координаты (0, 0, 0), вершина B имеет координаты (a, 0, 0), а вершина C имеет координаты (0, b, 0), где a и b - длины сторон треугольника ABC.

Теперь мы можем определить векторы с началом и концом в вершинах призмы:

1. Вектор AB:
Координаты начала вектора AB соответствуют координатам вершины A, то есть (0, 0, 0). Координаты конца вектора AB соответствуют координатам вершины B, то есть (a, 0, 0). Следовательно, вектор AB имеет координаты (a - 0, 0 - 0, 0 - 0), или просто (a, 0, 0).

2. Вектор AC:
Координаты начала вектора AC соответствуют координатам вершины A, то есть (0, 0, 0). Координаты конца вектора AC соответствуют координатам вершины C, то есть (0, b, 0). Следовательно, вектор AC имеет координаты (0 - 0, b - 0, 0 - 0), или просто (0, b, 0).

3. Вектор BC:
Координаты начала вектора BC соответствуют координатам вершины B, то есть (a, 0, 0). Координаты конца вектора BC соответствуют координатам вершины C, то есть (0, b, 0). Следовательно, вектор BC имеет координаты (0 - a, b - 0, 0 - 0), или просто (-a, b, 0).

Таким образом, векторы с началом и концом в вершинах призмы, равные вектору АА, будут следующими:

1. Вектор AB с координатами (a, 0, 0).
2. Вектор AC с координатами (0, b, 0).
3. Вектор BC с координатами (-a, b, 0).