В тире имеется 5 винтовок №№ 1, 2, 3, 4, 5, различных по точности боя. Вероятность попадания в мишень из них равна для данного
стрелка соответственно 0.8, 0.9, 0.5, 0.4, 0.6. Стрелок бросает монету и, если
выпал герб, делает один выстрел из случайно выбранной винтовки с
нечетным номером. В противном случае он стреляет из случайно выбранной
винтовки с четным номером.
(а) Чему равна вероятность попадания в мишень?
(б) Попадание произошло. Какова вероятность того, что была выбрана 2я винтовка?

Ответы

vfeukb59Pavek 15.02.2022 07:57

Пусть событие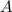 - "произошло попадание", а событие 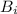B_i - "для стрельбы была выбрана i-ая винтовка".

Найдем вероятности событий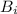 B_i .

По условию, выбор винтовки зависит от результата подбрасывания монеты. Пусть, на монете выпал герб, причем мы знаем, что герб выпадает с вероятностью $\dfrac{1}{2}$ . В этом случае, винтовка выбирается из трех (с нечетными номерами - 1, 3 и 5). Выбор винтовок равновероятный, поэтому вероятность выбрать каждую из этих винтовок после подбрасывания монеты равна $\dfrac{1}{3}$ . Итого, для выбора каждой из этих винтовок должны произойти два события: должен выпасть герб и винтовку должны выбрать из списка нечетных винтовок. Значит:

$B_1=B_3=B_5=\dfrac{1}{2} \cdot\dfrac{1}{3} =\dfrac{1}{6}$

Если на монете не выпал герб, что также происходит с вероятностью $\dfrac{1}{2}$ , то винтовка будет выбираться из двух (с четными номерами - 2 или 4). Выбор винтовок по-прежнему равновероятный, поэтому вероятность выбрать каждую из этих винтовок после подбрасывания монеты равна $\dfrac{1}{2}$ . В результате, для выбора каждой из этих винтовок должны произойти два события: не должен выпасть герб и винтовку должны выбрать из списка четных винтовок. Значит:

$B_2=B_4=\dfrac{1}{2} \cdot\dfrac{1}{2} =\dfrac{1}{4}$

Распишем, с какой вероятностью стрелок попадает в мишень. Эта вероятностью складывается из суммы попарных произведений вероятности выбора очередной винтовки и вероятности попадания из этой винтовки:

Вероятности попадания из винтовок даны по условию:

$P(A|B_1)=0.8;\ P(A|B_2)=0.9;\ P(A|B_3)=0.5;\\ P(A|B_4)=0.4;\ P(A|B_5)=0.6$

Находим вероятности попадания в мишень:

$P(A)=\dfrac{1}{6} \cdot 0.8+\dfrac{1}{4} \cdot 0.9+\dfrac{1}{6} \cdot 0.5+\dfrac{1}{4} \cdot 0.4+\dfrac{1}{6} \cdot 0.6=$

$=\dfrac{1}{6} \cdot (0.8+0.5+0.6)+\dfrac{1}{4} \cdot (0.9+0.4)=\dfrac{1.9}{6} +\dfrac{1.3}{4} =\dfrac{38}{120} +\dfrac{39}{120} =\boxed{\dfrac{77}{120} }$

Для ответа на второй вопрос воспользуемся формулой Байеса:

$P(B_2|A)\cdot P(A)=P(A|B_2)\cdot P(B_2)$

$P(B_2|A)=\dfrac{P(A|B_2)\cdot P(B_2)}{P(A)}$

Все величины известны. Поэтому, подставляем:

$P(B_2|A)=\dfrac{0.9\cdot \dfrac{1}{4} }{\dfrac{77}{120} }=\dfrac{9}{40} :\dfrac{77}{120} =\dfrac{9\cdot120}{40\cdot77}=\dfrac{9\cdot3}{77}=\boxed{\dfrac{27}{77}}$