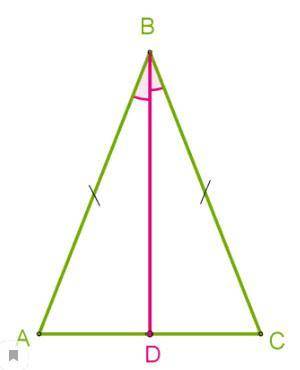
В равнобедренном треугольнике с длиной основания 19 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.

Рассмотрим треугольники ΔABD и Δ ___ (треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ ___;

2. так как проведена биссектриса, то ∡ ___= ∡ CBD;

3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC —___.

По второму признаку равенства треугольников ΔABD и ΔCBD равны.

Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.

AD=___см.

radchenkoalink    3   26.05.2020 11:17    84