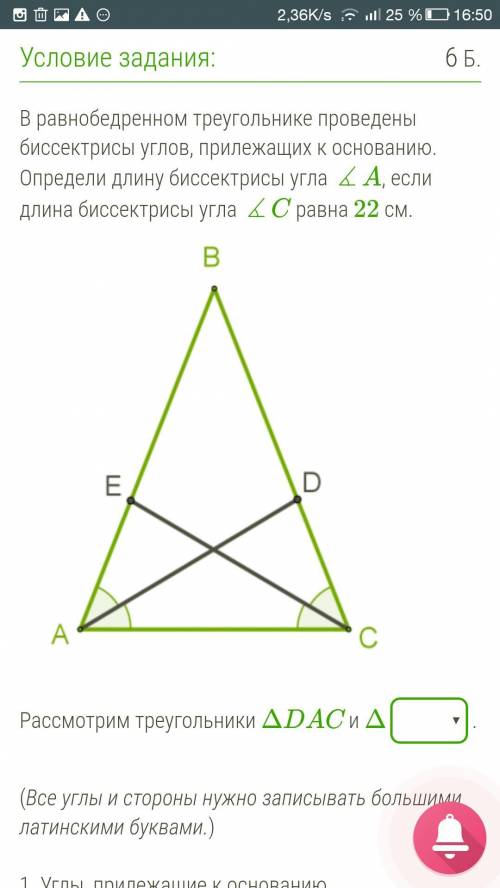
В равнобедренном треугольнике проведены биссектрисы углов, прилежащих к основанию. Определи длину биссектрисы угла ∡A, если длина биссектрисы угла ∡C равна 22 см. Pazime21_uzd.png Рассмотрим треугольники ΔDAC и Δ . (Все углы и стороны нужно записывать большими латинскими буквами.) 1. Углы, прилежащие к основанию равнобедренного треугольника, . Так как данный треугольник равнобедренный, то ∡B = ∡BCA. 2. Так как проведены биссектрисы этих углов, справедливо, что ∡ =∡DAC=∡DCE= ∡ . 3. У рассматриваемых треугольников общая сторона . Значит, треугольники равны по второму признаку равенства треугольников. У равных треугольников равны все соответствующие элементы, в том числе стороны = . Длина искомой биссектрисы см.

Для решения этой задачи, давайте взглянем на данную информацию и решим ее пошагово:

1. Поскольку у нас равнобедренный треугольник (AB = AC), углы, прилежащие к основанию (BC), также равны (∡B = ∡BCA).

2. Также нам известно, что проведены биссектрисы углов, прилежащих к основанию (BD и BE). Это означает, что угол ∡D совпадает с углом ∡DCE. И длина биссектрисы угла ∡C равна 22 см.

3. Рассмотрим треугольники ΔDAC и ΔBCE. Они имеют общую сторону DC и равны по второму признаку равенства треугольников (обе биссектрисы проведены из одного и того же угла).

4. Из равенства треугольников ΔDAC и ΔBCE следует, что соответствующие стороны равны. Следовательно, BD = CE.

5. Теперь мы знаем, что у нас равенство пар сторон BC = CE и BD = DC.

6. Рассмотрим треугольник ΔBED. Он является равнобедренным, так как BD = DC. Значит, его углы ∡DBE и ∡DEB равны.

7. Так как ∡DCE = 22° и угол ∡DEB является вертикальным углом к ∡DCE, он также равен 22°.

8. Из равенства ∡DEB = ∡DBE = 22° следует, что треугольник ΔBED равносторонний.

9. Теперь мы знаем, что углы ∡DBE, ∡BED и ∡EBD в равностороннем треугольнике ΔBED равны 60°.

10. Чтобы найти длину биссектрисы угла ∡A, нам нужно рассмотреть треугольник ΔBAD. Угол ∡ADB является вертикальным углом к ∡DBE и равен 60°.

11. Теперь у нас есть два угла треугольника ΔBAD (∡ADB и ∡BAD) и нужно найти третий угол ∡ABD (угол против основания треугольника).

12. Сумма углов треугольника всегда равна 180°, поэтому ∡ABD = 180° - (∡ADB + ∡BAD).

13. Подставим известные значения: ∡ABD = 180° - (60° + 60°) = 60°.

14. Таким образом, у нас есть два равных угла ∡ABD и ∡DBE в треугольнике ΔBAD.

15. Из равенства углов следует, что треугольник ΔBAD также равнобедренный.

16. Теперь у нас есть равенство BC = CE. Следовательно, BC = 22 см.

17. Для нахождения длины биссектрисы угла ∡A можно использовать теорему биссектрисы, которая гласит: длина биссектрисы угла A равна произведению двух боковых сторон (BD и DC), деленному на сумму этих сторон (BD + DC) и умноженному на косинус половины угла A.

18. В нашем случае у нас есть BD = DC = BC/2 (поскольку ΔBED является равнобедренным треугольником со сторонами BD, DC и BE, а BD = DC).

19. Подставим известные значения в формулу длины биссектрисы:
∠A = 60° (половина угла А)
BD = DC = 22 см
BC = 22 см (из равенства BC = CE)

Имеем: длина биссектрисы угла ∡A = (22 * 22) / (22 + 22) * cos(60°).
Посчитаем это выражение:

Длина биссектрисы угла ∡A = (484) / (44) * cos(60°)
= 11 * cos(60°).

20. Найдем значение cos(60°):
cos(60°) = 1/2.

Подставим это значение в формулу:
Длина биссектрисы угла ∡A = 11 * (1/2)
= 11/2
= 5.5 см.

Итак, длина биссектрисы угла ∡A равна 5.5 см.