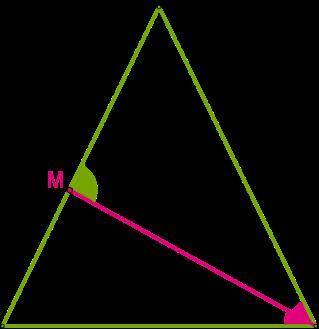
В равнобедренном треугольнике NLC проведена биссектриса CM угла C у основания NC, ∡ CML = 69°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
Другие вопросы по теме Алгебра
Популярные вопросы
- Денсаулық-зор байлық составить монолог на казахском с переводом на...
2 - Почему Николай Плужников решил выйти к немцам?...
3 - Питаются ли муравьи жнецы другими насекомыми...
3 - На якому поверсі булинку вода з під кранів витікатиме під більшим тиском:...
2 - Вычислите давление и силу давления керосина на дно бака площадью 10м2...
2 - О чем заставляет задуматься повесть «Шинель» и повесть «После бала...
2 - Вы получили письмо от своего новозеландского друга по переписке Шейлы,...
3 - Найдите сумму первых шестнадцати членов арифметической прогрессии,...
3 - Автомобиль ч. со скоростью 48,5 км/ч и 5 ч. со скоростью 59,6 км/ч....
1 - Рассказ толстый и тонкий Анализ и интерпретация Задание: Проанализируйте...
3
1. Свойство равнобедренного треугольника гласит, что биссектриса угла при основании делит противолежащую сторону на две равные части. То есть, в данном случае, длина отрезка CM равна длине отрезка ML.
2. Свойство биссектрисы гласит, что она делит противолежащий угол на два равных.
Исходя из этих свойств, мы можем сделать следующие выводы:
1. ∠MCN = ∠MCL, так как это углы смежные с равными сторонами.
2. ∠MCN + ∠MCL = ∠NCL, так как сумма углов треугольника равна 180°.
3. Следовательно, ∠NCL = ∠MCL + ∠MCL = 2∠MCL.
Теперь, нам осталось найти величины ∠MCL и ∠NCL.
Из условия задачи, нам дано, что ∠CML = 69°. Мы можем найти величину ∠MCL с помощью следующих вычислений:
∠MCL = 180° - ∠CML
∠MCL = 180° - 69°
∠MCL = 111°
Таким образом, мы нашли величину ∠MCL.
Теперь, чтобы найти величину ∠NCL, мы можем использовать следующее равенство: ∠NCL = 2∠MCL.
∠NCL = 2 * 111°
∠NCL = 222°
Таким образом, мы нашли величину ∠NCL.
Итак, ответ на задачу: величина угла ∠MCL равна 111°, а величина угла ∠NCL равна 222°.