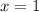В кривой в точке с абсциссой проведена касательная. 1.Определите угловой коэффициент касательной в этой точке

2.Определите ординату точки касания

3.Составьте уравнение касательной к кривой в этой точке

Добрый день, школьник! Давай решим задачу по нахождению углового коэффициента касательной к кривой в заданной точке, ординаты точки касания и составлению уравнения касательной.

1. Определение углового коэффициента касательной:
Для нахождения углового коэффициента касательной необходимо найти производную функции в данной точке. В данном случае у нас дана функция кривой y=x^2 - x - 12, поэтому нам нужно найти производную этой функции. Производная функции y=x^2 - x - 12 находится с помощью правила дифференцирования степенной функции: для функции y=x^n производная равна n*x^(n-1).

y' = 2x - 1

Теперь подставим значение x=1 в полученную производную:

y' = 2*1 - 1 = 2 - 1 = 1

Получаем, что угловой коэффициент касательной в данной точке равен 1.

2. Определение ординаты точки касания:
Для нахождения ординаты точки касания необходимо подставить значение x=1 в исходную функцию.

y = (1)^2 - 1 - 12 = 1 - 1 - 12 = -12

Получаем, что ордината точки касания равна -12.

3. Составление уравнения касательной:
Касательная к кривой в данной точке имеет уравнение вида y = kx + b, где k - угловой коэффициент, а b - свободный член.

У нас уже известно, что угловой коэффициент равен 1. Осталось найти свободный член b. Для этого подставим в уравнение координаты точки касания, которые нам известны: x=1 и y=-12.

-12 = 1*1 + b
-12 = 1 + b
b = -12 - 1
b = -13

Получаем, что свободный член b равен -13.

Таким образом, уравнение касательной к кривой в данной точке имеет вид y = x - 13.

Надеюсь, я смог достаточно подробно объяснить решение этой задачи и ответить на твой вопрос. Если у тебя еще остались вопросы, не стесняйся задавать их!