1. Алгебра
  2. в какой точке касательная,

в какой точке касательная, проведенная к графику функции у=е^2х+1-1 будет параллельна прямой у=2х+3?​

джемре джемре    1   04.06.2021 07:47    1

Ответы
Aleks2281338 Aleks2281338  04.07.2021 07:47

Угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания.

y=e^{2x+1}-1\ \ \ \to \ \ \ y'(x)=2e^{2x+1}\\\\y=2x+3\ \ \to \ \ \ k=2\\\\y'(x_0)=k\ \ \Rightarrow \ \ \ 2e^{2x+1}=2\ \ ,\\\\e^{2x+1}=1\ \ ,\ \ e^{2x+1}=e^0\ \ ,\ \ 2x+1=0\ \ ,\ \ x_0=-\dfrac{1}{2}\\\\y_0=e^{2\cdot (-\frac{1}{2})+1}-1=e^0-1=1-1=0

Точка, в которой  касательная проведенная к графику функции будет параллельна заданной прямой, имеет координаты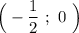  \Big(-\dfrac{1}{2} \ ;\ 0\ \Big) .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
killpvpglava killpvpglava  08.05.2020 12:50
Побудуйте графік функції у=1/6х-2. Знайти усі значення аргументу що б значення функції = 1) 0 2)+ 3)-...
Биіккесамға Биіккесамға  08.05.2020 12:59
Алгебра, решите очень нужно!...
napol2011 napol2011  08.05.2020 12:59
При каких значениях b и c прямые y=8x и y=−13x являются касательными к графику функции f(x)=x^2+bx+c?...
sasha21314154 sasha21314154  08.05.2020 13:00
Знайдіть sin α, якщо cos α = 21∕29...
Aelly Aelly  08.05.2020 13:00
16х/sqrt x-10 ((x-10) под корнем). Найти ОДЗ, желательно с объяснением...
кузя1310 кузя1310  08.04.2021 22:59
Решить уравнение m^3 + 3m^2 = 4^m + 12...
Inna050798 Inna050798  08.04.2021 22:58
Если не сложно запишите решение на листочке)​...
Tima411 Tima411  08.04.2021 22:54
Знайти корінь рівняння -14х=7​...
ghj42 ghj42  08.04.2021 22:53
Одна із сторін прямокутника на 6 см менша за другу. Знайти периметр, якщо площа дорівнює 72см^2. Використовувати квадратні рівняння...
SFDFGDDDDFGDGD SFDFGDDDDFGDGD  08.04.2021 22:51
Знайти корінь рівняння 9х-7=6х+14​...

Популярные вопросы