:в какой многочлен можно преобразовать выражение 1) (а-2)^2-2a(2a-2)= 2) (a-1)^2-a(2a-2)= 3) (a-3)^2-6a(a-1)= 4) (2a-1)^2-4a(a+1)= 5) (a-4)^2-2a(a-4)= примечание: пишите выражением,и ^2-это значит что скобка взята в
Другие вопросы по теме Алгебра
Популярные вопросы
- Кароткое сочинение на тему мой любимый день зимы...
3 - Какие моря, океаны, заливы, проливы омывают россию...
2 - 1) докажите, что при ярославе мудром произошло усиление власти киевского...
3 - Рост кати 1м 75см. вытянувшись во весь рост,она спит под одеялом,длина...
1 - Из 15 метров ткани сшили 10 платьев.сколько платьев можно сшить из...
1 - Выражение (9-в)(9+-в)(9+3в+2в2) и найдите его значение при в=-1...
3 - Что такое трудовой договор каковы условия его заключения и расторжения...
2 - Это растение своими корнями сдерживает движение песка...
2 - Счего пища начинает перевариваться в ротовой полости?...
3 - Закончи предложение глава нашего государства законы рф разрабатывают...
2
Что конкретно неясно? Все задания - типовые. В каждом есть формула с. у. - квадрат разности, а так же скобки, которые нужно раскрыть, используя правило умножения одночлена на многочлен.
Чтобы решить любое из этих заданий, требуется
1) Раскрыть скобки, используя правило умн. одночлена на многочлен, а также формулу, помня, что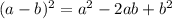 .
.
2) Привести подобные слагаемые.
1.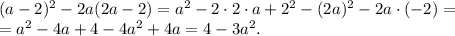
2.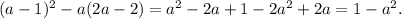
3.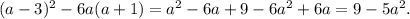
4.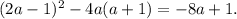
5.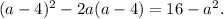
1) (а-2)^2-2a(2a-2)=a² - 4a +4 - 4a²+ 4a = 4 - 3a²
2) (a-1)^2-a(2a-2)= a² - 2a +1 - 2a² + 2a = 1 - a² = (1-a)(1+a)
3) (a-3)^2-6a(a-1)= a² - 6a + 9 - 6a² + 6a = 9 - 5a²
4) (2a-1)^2-4a(a+1)= 4a² - 4a + 1 - 4a² - 4a = 1 - 8a
5) (a-4)^2-2a(a-4)= a² - 8a + 16 - 2a² + 8a = 16 - a² = (4-a)(4+a)