1. Алгебра
  2. В геометрической прогрессии

В геометрической прогрессии все члены отличные от нуля числа. Знаменатель не равен 1 и -1. Разность одиннадцатого и пятого членов прогрессии больше разности седьмого и пятого в 21 раз. Сумма первых восьми членов равна 1020.

Найдите четвёртый член данной прогрессии.

falala1 falala1    2   24.07.2022 13:17    0

Ответы
vail12 vail12  24.07.2022 13:18

b_{11}-b_5=21(b_7-b_5)\\S_{8}=1020\\b_4= \;?

b_1q^{10}-b_1q^{4}=21b_1q^6-21b_1q^4\\q^{10}-q^4=21q^6-21q^4\\q^6-1=21q^2-21\\q^6-21q^2+20=0

(q^2)^3-21q^2+20=0\\

Сделаем замену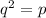 q^2=p

p^3-21p+20=0

Корень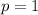  p=1 сразу подбирается, далее разделим уголком этот трёхчлен на двучлен 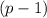(p-1) (см. фото):

p^3-21p+20=(p-1)(p^2+p-20)=0

Решим квадратное уравнение:

p^2+p-20=0\\D=(-1)^2+4 \cdot 20=81\\p_1=\dfrac{-1+9}{2}=4\\p_2=\dfrac{-1-9}{2}=-5

Отрицательный корень не подходит, т. к.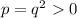 p=q^2 0:

q^2=4\\q_1=2\\q_2=-2

Первый случай q=2:

S_{8}=\dfrac{b_1(q^8-1)}{q-1}=\dfrac{b_1(2^8-1)}{2-1}=b_1(256-1)=255b_1=1020\\b_1=4\\b_4=b_1q^3=4\cdot 2^3=4 \cdot 8=32

Второй случай q=-2:

S_8=\dfrac{b_1((-2)^8-1)}{-2-1}=-\dfrac{255}{3}b_1=1020\\-\dfrac{1}{3}b_1=4\\b_1=-12\\b_4=b_1q^3=-12 \cdot (-2)^3=12 \cdot 8=96

ответ: 32 либо 96.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ketrindemey5 ketrindemey5  27.06.2019 22:40
Для функции f(x)=1/х3 найдите первообразную,график которой проходит через точку a(1,0)...
Niiiiklou Niiiiklou  27.06.2019 22:40
Help! найдите значение выражения : 2^log2 (3) -1...
severin4568 severin4568  27.06.2019 22:40
Разложите трёх член на множители 36c^2+ 156cm+ 169m^2...
diaries1 diaries1  08.07.2019 07:10
Куртка стоила на 1500руб меньше, чем костюм. во время сезонной распродажи куртка подешевела на 10%, а костюм на 20%, после чего куртку и костюм вместе можно было приобрести...
sofiavasulyuk sofiavasulyuk  08.07.2019 07:10
Павел, живущий в 50 км от места проведения соревнований по футболу, в кото- рых он участвовал, решил поехать на турнир на велосипеде. рассчитав время, он проехал первые...
Bogura Bogura  08.07.2019 07:10
Какая из точек принадлежит графику функций заданной формулой y=-3x 1) a(2(6) 2) в (-2; 6) 3) с(-2; -6) 4)д(2; 1...
ksusha293 ksusha293  20.07.2019 01:10
Какое из чисел больше: √5+√13 или 2+√14?...
IoneAngel IoneAngel  20.07.2019 01:10
Решите уровнения: х^2+4=5x 3x^2=x+4 x+6=x^2 4x^2+x-5=0 2x^2-28x+66=0...
nshtvr nshtvr  20.07.2019 01:10
Решите систему уравнений. 10 ! ! :...
Fox125123 Fox125123  20.07.2019 01:10
1). (m-n)(m^2+mn+n^2) 2). (x+y)(x^2-xy+y^2) 3). (3x+r)(9x^2-3xr+r^2) 4). (p-5q)(p^2+5pq+25q^2) 5). (1-m)(1+m+m^2) 6). (x+4)(x^2-4x+16)...

Популярные вопросы