В геометрической прогрессии (bn) известно, что q= 2, а S3=635
a)Найдите первый член и знаменатель этой прогрессии
b) Найдите сумму первых восьми членов геометрической прогрессии
Другие вопросы по теме Алгебра
Популярные вопросы
- Пиши ответ! заранее ! 1. какие питательные вещества откладываются про...
1 - 86см-(33см -26см)+7дм3см выразить в дм и см...
1 - 9/14 x - 1/7 x - 0,5 x = 9/14 x - 2/14 x - 0,5 x = 7/14 x - 0,5 x =...
1 - 1.записать арабскими цифрами: xvii, lii, mdxxxiii. 2.записать римскими...
2 - Составьте уравнение реакций взаимодействия s+ae s+c h2so4+zn cu(oh)2...
1 - Корганам выделения моллюсков относят а) печень б) почку в) кишечник...
2 - Какие жизненные события легли в основу стихотворения лермонтова тучки...
3 - Морфемный разбор слова сопротивляешься...
1 - Какие аргументы можно в сочинение на тему дети и война ?...
3 - Кокой падеж у слова струится,берегам. я буду с вами добра...
2
По условию знаменатель прогрессии известен:
Сумма первых n членов геометрической прогрессии:
По условию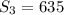 :
:
Находим первый член:
Найдем сумму первых 8 членов: